The real reason doesn't have to do with sines of angles, but with the wave nature of light.
The images below show a close-up to what happens when a wave reaches an interface at which it is partially reflected and partially transmitted (lifted from my answer to Does light reflect if incident at exactly the critical angle?):




The complete situation has three relevant waves: the incident wave, the reflected wave, and the transmitted wave, with the first two adding up to give an interference pattern in the incidence medium.
Each wave has the general form
$$
E(x,y,z,t) = \operatorname{Re}\left[E_0 \exp\left(i\left(k_x x + k_y y - \omega t\right)\right)\right]
$$
(where I've ignored the $z$ component by setting the incidence plane as the $x,y$ plane). Here the $x$ direction is the horizontal direction on the plots above $-$ i.e. the coordinate along the interface $-$ and $y$ is the direction normal to the interface. Within this wave picture, Snell's law (and all of its consequences) follows from a small core set of physical principles:
The behaviour of all the waves along the interface must match, i.e. the transverse dependence of the wave, given by the factor of $$\exp(i k_x x),$$ must be the same for the reflected and transmitted waves as it is for the incident wave. This means that the transverse component of the wavevector, $k_x$, must be the same for all three waves.
(Similarly, the same must be true for the temporal dependence, $\exp(-i\omega t)$, which means that the temporal frequency cannot change across the interface.)
The magnitude of the wavevectors on each of the relevant media must be such that the waves obey the relevant wave equation, which then requires that
$$
\frac{k_1^2}{n_1^2} = \frac{\omega^2}{c^2} = \frac{k_2^2}{n_2^2}.
$$
When you have internal reflection, this means that $n_1>n_2$, so that $n = n_1/n_2>1$, and therefore
$$k_1^2 = n^2 k_2^2>k_2^2.$$
At high incidence angles, a large fraction of $k_1^2 = k_{1x}^2 + k_{1y}^2$ comes from the transverse component $k_{1x}^2$, which must also match $k_{2x}^2 = k_x^2 = k_{1x}^2$, so that
$$k_1^2 = k_{x}^2 + k_{1y}^2 = n^2 ( k_{x}^2 + k_{2y}^2) > k_{x}^2 + k_{2y}^2 = k_2^2.$$
If $k_{1x}^2$ is large enough, this requires $k_{2x}^2$ to be larger and larger, while still requiring the total wavevector $k_2^2$ to be kept below a certain bound, and at some point this cannot be sustained, and there is no propagating wave that can fulfill these relationships.
More geometrically, as the incident wave becomes more and more tilted, its transverse wavelength along the boundary ($\lambda_\perp = 2\pi/k_x$) becomes shorter and shorter, and at some point it becomes shorter than the wavelength of light in the thinner medium, $\lambda_2 = \frac{2\pi}{k_2} = n\frac{2\pi}{k_1} = n\lambda_1 > \lambda_1$, and that wave is no longer supported.
This is then seen geometrically as the wave reaches the critical angle,




and then past the critical angle into the total-internal-reflection regime,



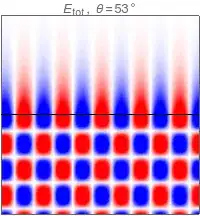
where you can see that the transverse wavelength is now shorter than $\lambda_2$; in other words, $k_{2x}^2 > k_2$, which requires $k_{2y}^2$ to be negative (!). Thus, in the wave picture, $k_{2y}$ needs to be imaginary, so that the transmitted wave is an evanescent wave, with the "oscillatory" factor $\exp(ik_y y) = \exp(-\kappa y)$ now taking on an exponential decay. (This is generally extremely fast, which is why this evanescent wave is normally completely ignored within the ray picture of geometric optics.)
Hopefully that helps clarify what's going on in this process.











