Why do we have heavy and light hole bands in semiconductors?

Question

On the topic of the valence band of a semiconductor (in this example GaAS), it is the case that the valence band has some structure to it. As shown in the illustration below, we see that at the $\Gamma$ point there are three visible bands: the spin orbit split off band (due to the effect of the spin orbit interaction) and above that the heavy and light hole bands.

Now, my question is rather simple: why do we observe these different light and heavy hole bands? I'm aware of the fact that heavy and light refers to their effective mass (inversely related to the curvature of the bands), and these are thus bands of holes with a different effective mass, but what is the cause of their masses being different?

Answer 1

To delve more deeply into the origin of the various bands, you should go look at the literature where these bands are calculated. The classic reference for silicon and germanium is Energy-Band Structure of Germanium and Silicon: the k.p Method. Since this is still fairly early in band structure calculations, they do walk you through how the Hamiltonian is built up from the various terms.

It should also be noted that the parabolic approximation is only valid near the symmetry points - in general the bands are not simple parabolas.

Answer 2

To summarize, I found this phenomenon to be pretty well explained by Fang et. al. in 1. I will relate more information from a few sources here.

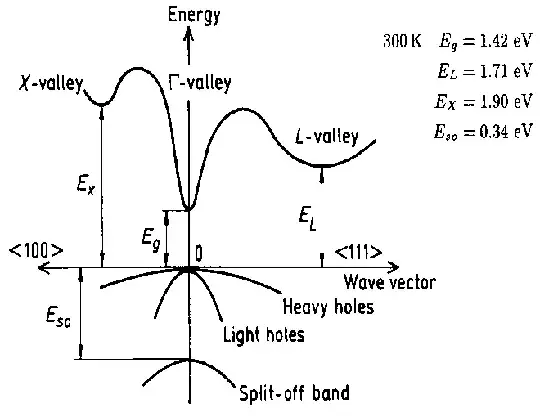
In the Hamiltonian for the holes in the valence bands of III–V compound semiconductors, there is a strong spin-orbit coupling between the crystal momentum and hole angular momentum. The atomic $J = 3/2$ states have a four-fold degeneracy (see 1 for details on why), and this degeneracy is further split into two doubly degenerate bands by the crystal-hole momentum coupling. The higher valence bands are denoted "heavy" and the lower are denoted "light". The splitting between the heavy and light bands is comparable to the kinetic energy from the Hamiltonian describing them - the Luttinger Hamiltonian. Technically, the splitting is determined by these Luttinger parameters ($\gamma$).

$$ H_{L} \left(\mathbf{k} \right) = - \left( \gamma_{1} + \frac{5}{2} \gamma_{2} \right) \frac{\hbar^{2} \mathbf{k}^{2}}{2 m_{0}} + \gamma_{2} \frac{\hbar^{2}}{2 m_{0}} \left( k_{x}^{2} J_{x}^{2} + k_{y}^{2} J_{y}^{2} + k_{z}^{2} J_{z}^{2} \right) + \gamma_{3} \frac{\hbar^{2}}{2 m_{0}} \left( \left\{ k_{x}, k_{y} \right\} \left\{ J_{x}, J_{y} \right\} + c.p.\right)$$

Here, $\left\{ J_{i} \right\}$ are spin-$3/2$ matrices, $\gamma$ are so-called Luttinger parameters, $m_{0}$ the bare electron mass, $\left\{ A, B \right\} = \frac{AB + BA}{2}$, c.p. terms for the cyclic permutations of $x$, $y$, $z$.

In terms of what why we can see this splitting (more concretely), [2] gives an example where the heavy and light hole splitting in a group-IV quantum dot is given by the perpendicular confinement of the quantum dot. In this example, the diagonal terms of the barrier configuration change the heavy hole - light hole splitting by a constant.

In examples like this, you can think of the quantum dot as approximating a 3D quantum particle in a box. The vertical confinement in [2] is achieved by a gate electric field in the "growth" direction - the literal direction in which a Germanium trace is grown on a substrate in the lab. The lateral confinement is modeled by an in-plane parabolic potential well.

In terms of why we see this (more generally), I need to refer myself to [3] and [4] for group theoretic details, which are now on my reading list.

1. Fang, Y., Philippopoulos, P., Culcer, D., Coish, W. A., & Chesi, S. (2023). Recent advances in Hole-spin qubits. Materials for Quantum Technology, 3(1), 012003. https://doi.org/10.1088/2633-4356/acb87e

2. Wang, Z., Marcellina, E., Hamilton, A. R., Cullen, J. H., Rogge, S., Salfi, J., & Culcer, D. (2021). Optimal Operation Points for ultrafast, highly coherent GE hole spin-orbit qubits. Npj Quantum Information, 7(1). https://doi.org/10.1038/s41534-021-00386-2

3. Elliott, R. J. (1964). The properties of the thirty-Two point groups. Cryogenics, 4(5), 334. https://doi.org/10.1016/0011-2275(64)90116-x

4. Dresselhaus, M. S., Dresselhaus, G., & Jorio, A. (2010). Group theory: Application to the physics of Condensed Matter. Springer-Verlag.

Answer 3

For example, in the case of common zincblende structure, under the periodic crystal potential the valence band is split into heavy hole($\Gamma_{8}$) band and light hole ($\Gamma_{8}$) band, and split-off ($\Gamma_{7}$) band at the states of Brillouin zone center ($\Gamma$ point).