Relationship between applied and normal force?

Question

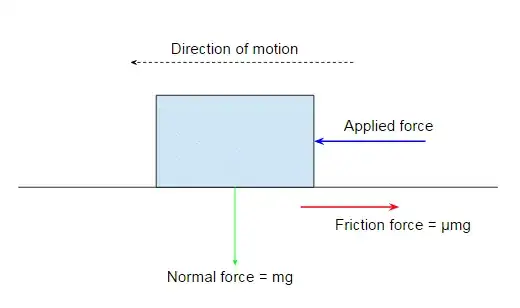
After watching and reading many explanations on friction, normal force and newton's laws, I am more confused than I was before... I have a simple question:

• Why is the normal force of an object that is moved across a horizontal plane equal to the applied force when the velocity is constant?

First, I thought the normal force is not equal to the applied force but to the force of the weight which points downward in a body diagram. But then I figured this can't always be true because the normal force of inclined surfaces is not directly opposite to the force of the weight. But I don't understand why the normal force should be equal to the friction force. The Force of friction is $F = \mu.mg$ ($\mu$ = friction, $m$ = mass, $g$ = gravity), right? And this is the same as saying the Force of friction is the same as the applied force, right? - But what is the formula of the normal force in this case?

• How can I proof mathematically that the $Fapplied = Fnormal$?

• I always read the friction force is proportional to the normal force but why?

It seems like nobody can give me a simple explanation why this is true.

Answer 1

Let's draw a quick diagram to make it clear what we're talking about:

The condition for constant velocity is that the applied force $F$ and frictional forces $\mu mg$ are equal so:

$$ F = \mu mg $$

As you thought, the normal force is not equal to the applied force - well, not unless the coefficient of friction $\mu$ happens to be equal to one.

The equation relating the frictional force $F_f$ to the normal force $F_n$:

$$ F_f = \mu F_n $$

is generally called Amonton's law. However this is an effective law not a basic principle, and in practice applies only in limited conditions. Why Amonton's law is a useful approximation is discussed in Why is the equation for friction so simple? and in more detail in the paper On the origin of Amonton’s friction law by Persson et al, J. Phys.: Condens. Matter 20 (2008) 395006.