Particle accelerators reaching light speed

Question

I just have a question in mind that's stuck in my head, and it's why particle accelerators cannot accelerate any particle to the speed of light. I'm assuming it involves Einstien's theory of relativity.

Answer 1

They get awfully close. Rather than talk about the "velocity" of particles, the folks at CERN end up talking about the "energy" - because once you're at 0.99 c and above, your energy continues to increase (basically, mass increases) but the velocity doesn't - much. That is expressed by the factor $$\gamma = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$ yes, it is a consequence of the theory of relativity. The current record of energy is about 7 TeV for a lead nucleus which has a "rest mass" of ~0.2 TV, meaning $\gamma=14$ and v=0.997 c

In 2015, the LHC was running with 6.5 TeV protons (link); since their mass is much smaller than the mass of lead (938 MeV), this corresponds to a $\gamma$ of about 6900, and $$v = 0.9997 c$$

Answer 2

I just have a question in mind that's stuck in my head, and it's why particle accelerators cannot accelerate any particle to the speed of light.

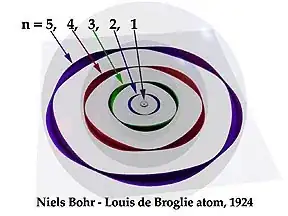
It's because of the wave nature of matter. We can quite literally make matter out of light waves in pair production. Then we can diffract electrons. And in atomic orbitals electrons "exist as standing waves". Images like this de Broglie atom by Kenneth Snelson are a bit of an oversimplification, but they get the point across:

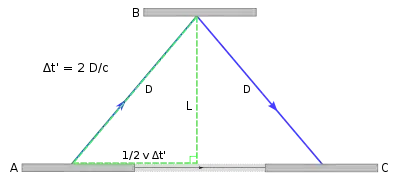
Floris referred to the Lorentz factor. Have a look at the simple inference of time dilation due to relative velocity in the Wikipedia time dilation article. The Lorentz factor can be derived from Pythagoras's theorem. The hypotenuse of a right-angled triangle represents the lightpath where c=1 in natural units. The base represents your speed as a fraction of c:

_{Public domain image by Mdd4696, see Wikipedia}

The height gives the Lorentz factor $\gamma$, and we use a reciprocal when appropriate, for example to distinguish time dilation from length contraction.

I'm assuming it involves Einstein's theory of relativity.

It does. The mass of a body is a measure of its energy-content. A radiating body loses mass. In electron-positron annihilation to gamma photons, two radiating bodies lose mass. We have evidence of things like magnetic moment and electron spin where the Einstein de Haas effect demonstrates that "spin angular momentum is indeed of the same nature as the angular momentum of rotating bodies as conceived in classical mechanics". So look at the picture of the de Broglie atom again and think of the electron as a wave going round the n=1 circle: O. Then turn the circle on its side like so: | . Then move it, and it resembles the light beam above: /\. It can be likened to stretching out a helical spring. It gets harder and harder to stretch it out, and you can't stretch it straighter than straight. In similar vein you can add more and more energy but you can't get the electron moving faster than light.