why it moves in a elliptical orbit when it is moving with velocity more than the orbital velocity
The escape speed $v_{escape}$ is the minimum speed needed, for the object satellite to not follow an orbit. So, if the speed is higher than circular orbital speed (so it will not be a circle) but lower than escape velocity (so it will follow an orbit), then it will have to follow another kind of orbit, which happens to be elliptical.
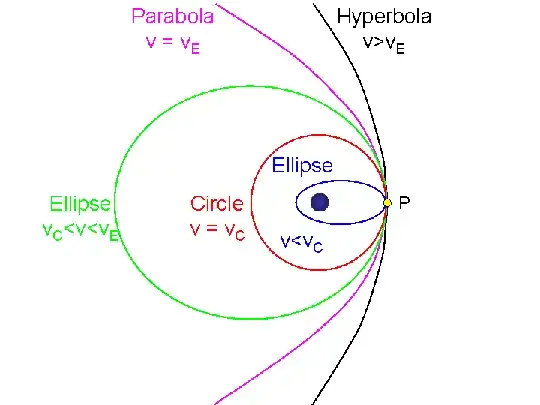source: http://www.astronomy.ohio-state.edu/~pogge/Ast161/Unit4/orbits.html
why is there a specific value of escape velocity
Shoot something away extremely fast and it will fly onwards away from Earth and never come back. If it was shot off fast enough, it might get so far away that it doesn't really feel gravity anymore of any significant amount.
Now instead throw something upwards. It will fall back. It has clearly not escaped gravity.
Somewhere in between the large and small velocity, there of course must be a velocity value, which is just the limit, the minimum needed value, to escape.
We call this limit the escape velocity.
why the escape velocity is √2 times the orbital velocity?
The explanation is simply mathematical, so view the derivation. It starts from the energy conservation, where:
$$K_1+U_1=K_2+U_2$$
where point 1 is right after launch (so $v_1$ start speed) and point 2 is at some point infinitly far away. Infinitly far away, the potential energy is zero $U_2=0$. And if the object does escape, then the velocity will still be positive infinitly far away (it will forever continue moving) - exactly on the limit between escaping (where it keeps moving away) and not escaping (where it will return and would have negative velocity), the velocity will be zero $v_2=0$, so on this limit we have $K_2=0$.
$$K_1+U_1=0+0\\
\frac12 mv_1^2-\frac{Gm_{earth} m}{R}=0\\
v_1=v_{escape}=\sqrt{\frac{2Gm_{earth}}{R_{earth}}}$$
The start speed $v_1$ that fulfills this relationship is the speed, that exactly reaches this lower limit - that is the escape velocity $v_1=v_{escape}$.
That this expression is proportional to the circular orbital speed $v=\sqrt{\frac{GM_{earth}}{r}}$ is somewhat a coincidence, since that speed could be derived in a different way (from Neton's 2nd law).
