1

I was going through this link

http://physics.weber.edu/schroeder/mrr/MRRtalk.html

There it says

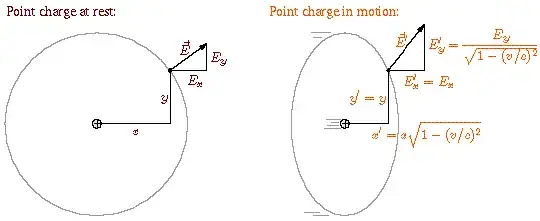
Now consider the electrostatic field of a point charge at rest, shown at left below. At every point on the circle (actually a sphere), the field has the same strength and points directly away from the particle.

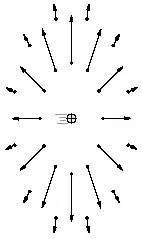
enter image description here

Field of a point charge, at rest and moving to the right If we put this system in motion to the right (shown at right), two things happen. The first is that the sphere gets length-contracted, flattened in the direction of motion. The second is that the components of the field perpendicular to the motion get stretched by the very same Lorentz factor. Therefore the field still points directly away from the point charge, but it's not the same in all directions: it's weaker in front of and behind the particle, and stronger to the sides, as shown below.

enter image description here

Field vectors around a point charge moving to the right

But I am not able to understand why the field perpendicular to the motion of charge gets stretched? Isn't it completely independent of how the field in other direction spreads? Shouldn't the $y$ direction always have?

$\LARGE\frac{E}{4\pi\epsilon_0 r^{2}}$

Inquisitive
  • 522

1 Answers1

1

The stretching of the electric field comes explicitly from the Lorentz Transform acting on the electromagnetic field tensor. The discussion here may be useful: http://bado-shanai.net/Map%20of%20Physics/mopLorentzTransEMField.htm . A bit of knowledge of vector calculus and perhaps even tensors is required to appreciate this explanation for the transformation of the E and B fields.

Also, the statement that the field is "weaker in front and back and stronger on the sides" doesn't make sense physically because the E and B fields parallel to the direction of motion are unaltered by a Lorentz transformation.

Loonuh
  • 663