3

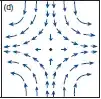
My text book on meteorology claims that a hyperbolic flow pattern is both divergence-free and irrotational:

enter image description here

(d) Hyperbolic flow that exhibits both diffluence and stretching, but is nondivergent because the two terms exactly cancel. Hyperbolic flow also exhibits both shear and curvature, but is irrotational (i.e., vorticity-free) because the two terms exactly cancel.

-- Wallace & Hobbs, Atmospheric Science, 2nd Ed, p 273

In my understanding, that can not be true:

  • I can obtain a very similar flow pattern from $ grad \ xy $.
  • Based on the uniqueness of Helmholtz decomposition, the only divergence-free, irrotational vector field should be $ \vec{f} = \vec{0} $.
  • Based on Helmholtz decomposition, any vector field $ \mathbf{u} $ can be represented as $ \mathbf{u} = \mathbf{v} + \mathbf{d} $ with $ \mathbf{v} = \nabla \phi $ and $ \mathbf{d} = \nabla \times \mathbf{A} $. As I understand it, the only divergence-free ( $ \mathbf{v} = 0 $ ) and irrotational ( $ \mathbf{d} = 0 $ ) vector field can be $ \mathbf{u} = 0 $.

Am I missing something or is the text handwaving the math a little too much here?

Christian Aichinger
  • 395

1 Answers1

2

Based on Hodge-Helmholtz decomposition a vector field $\mathbf{u}$ can be expressed as the sum of an irrotational vector potential $\phi$ and a divergence-free vector field $\mathbf{d}$. $$\mathbf{u} = \nabla \phi + \mathbf{d}$$ For a flow to be irrotational it has to be able to be derived as the gradient of a vector potential $$\mathbf{u} = \nabla \phi$$ It also follows that is the flow is simply-connected and irrotational then $$\mathbf{u} = \nabla \times \mathbf{d}$$The difference field $\mathbf{u} - \mathbf{d}$ is irrotational therefore it can be resolved as a gradient of a vector potential $\phi$ by taking the divergence of the above equation. $$\nabla \cdot \mathbf{u} = \nabla^2\phi$$ A vector field satisfying the above equation in which both the lhs and rhs vanish and also satisfies the irrotational condition is both irrotational and divergence-free. Specifically $\nabla \cdot \mathbf{u} =0$ and $\nabla^2\phi = 0$ and $\mathbf{u} = \nabla \phi$. A possible function $\phi$ for which the vector field $\mathbf{u}$ can be derived from is a harmonic function.