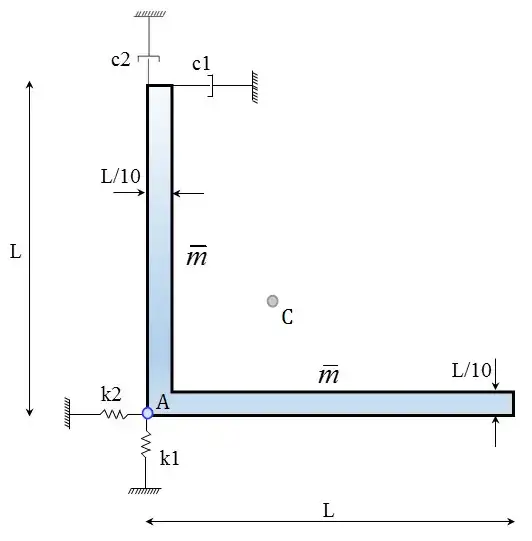
I want to derive equation of motion for the system shown in picture. How do I choose a generalized coordinate in order to calculate kinetic and potential energy of the system? I need the aforementioned quantities to implement Lagrange equations for determining the equation of motion. How many DOFs does the system has?
1 Answers
Consider the net forces $F_x$, $F_y$ and moments $M_A$ at a point A, let's say the corner of the beam
now consider the center of mass at a point C located at $(c_x,c_y)$ relative to A. This location changes in each time frame because it is measured from an inertial reference frame (and not in the body frame).
The three degree of freedom of the body can be the position of A $(x_A,y_A)$ and the orientation angle $\theta$. The equations of motion from a Newtonian point of view are
$$ \begin{align} F_x & = m \ddot{x}_A - m c_y \ddot{\theta} - m c_x \dot{\theta}^2 \\ F_y & = m \ddot{y}_A + m c_x \ddot{\theta} - m c_y \dot{\theta}^2 \\ M_A &= (I_C+ m (c_x^2+c_y^2)) \ddot{\theta} + m (c_x \ddot{y}_A - c_y \ddot{x}_A ) \end{align} $$
Where $m$ is the total mass, and $I_C$ is the mass moment of inertia about the center of mass. (See Derivation of Newton-Euler equations of motion for a derivation of the equations of motion not on the center of mass in 3D).
What you are interested in the motion due to the net forces at each frame which is
$$\begin{pmatrix} \ddot{x}_A \\ \ddot{y}_A \\ \ddot{\theta} \end{pmatrix} = \begin{vmatrix} \frac{1}{m} + \frac{c_y^2}{I_C} & - \frac{c_x c_y}{I_C} & \frac{c_y}{I_C} \\ - \frac{c_x c_y}{I_C} & \frac{1}{m} + \frac{c_x^2}{I_C} & -\frac{c_x}{I_C} \\ \frac{c_y}{I_C} & - \frac{c_x}{I_C} & \frac{1}{I_C} \end{vmatrix} \begin{pmatrix} F_x \\ F_y \\ M_A \end{pmatrix} + \begin{pmatrix} c_x \dot{\theta}^2 \\ c_y \dot{\theta}^2 \\ 0 \end{pmatrix} $$
The last part that is needed is to expressed the forces as a function of the degrees of freedom. For small movements you can estimate
$$ \begin{pmatrix} F_x = -k_2 x_A - c_1 (\dot{x}_A-L \dot{\theta}) \\ F_y = -k_1 y_A - c_2 (\dot{y}_A) - m g \\ M_A = - c_1 L (\dot{x}_A-L \dot{\theta}) - c_x m g \end{pmatrix}$$
- 40,139