13

Sometimes different but related things have the same name by some tradition or accident, causing a lot of headache to newcomers to a field.

I would like to come to clear terms with this: does the expression 'focal length' mean something distinct when applied to pinhole cameras vs. lens cameras?

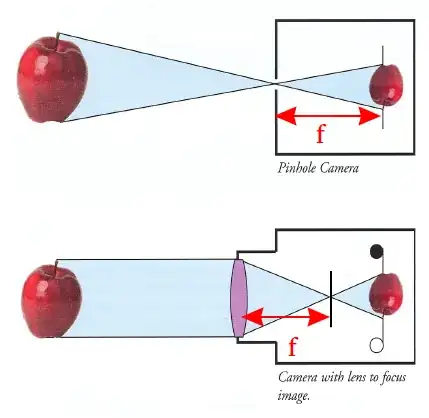
Focal length illustration

With pinhole cameras it's the distance from the pinhole to the image plane. With lenses, it's the distance from the lens to the point where parallel incoming rays meet. Why are these things called the same? Am I right that this is just clumsy nomenclature or are these related at the limit of some infinities?

EDIT: Apparently some other diagrams label the lens-to-image-plane as "focal distance". Is "focal distance" something else than "focal length"? Or are people using inconsistent definitions? Something's fishy here.

isarandi
  • 915
  • 2
  • 8
  • 14

3 Answers3

8

Focal length in Physics is a property of a lens usually labeled $f$. It doesn't depend on the distances to the object or image involved (though you may determine if from that information).

The distance from the lens to the image is the image distance, often labeled $q$ or $d_i$. If it's positive, there is a real image and that is where the film or sensor should be.

A pinhole camera doesn't have a lens. It has a focal length of $\infty$. This leads to a virtual image (negative $q$), but the pinhole gives it such a huge depth of field that you call place the film anywhere and get focus as if you had a real image.

Spirko
  • 1,031
4

While your sketch is correct, its scales may confuse you in this case. Do remember that, denoting the distances from the lens to the object and image plane by $z_o$ and $z_i$, respectively, we have $$\frac 1f = \frac{1}{z_o} + \frac{1}{z_i}.$$

Now in real world scenes, usually the camera dimensions are very small, so that $$z_o \gg z_i \Rightarrow f \approx z_i.$$ This means that a lensed camera with "focal point" at a distance $f$ from the lens can be geometrically thought of as a pinhole camera with "focal length" $f$. Of course the main difference is that since the lens in fact focuses many rays from the object to the same point on the image plane, the resulting intensity will be much higher. This approximation is very useful, however, when you try to figure the directions distances towards photographed objects.

Martin Weitzel
  • 3
yaronra
  • 56
0

Have a look to the beginning of this video https://www.youtube.com/watch?v=ecuDGXZjyl0 The presenter is trying to make links between the people comming from computer vision and optics and explicitely discuss this.

VojtaK
  • 131
  • 3