When I shine a beam of light at a mirror why does the ray go in the exact opposite direction (tested with protractor). Why does it not go back in exactly the same direction? The beam is of an unspecified wavelength, it was just shone from a lightbulb in a box with a slit of a few millimeters to let a beam of light shine through.
Asked
Active
Viewed 365 times
2 Answers
1
One quite general argument is one of symmetries and conserved quantities.
Light does carry momentum in the direction of propagation and momentum conservation is related to a symmetry: the homogeneity of space. (This result is a special case of the Noether-Theorem).
The mirror (idealized as being infinitely large and perfectly even) can be understood as a boundary condition, that breaks continuous translation symmetry only in one direction (let's call it $y$), while the $x$ and $z$ directions continue to be translation invariant.
This tells you, that the presence of the mirror cannot change $x$ and $z$ components of the propagation direction of the light, therefore the light beam does not return to its origin, unless it is perpendicular to the mirror.
The fact that the $y$ component of the direction is exactly reversed is a bit more tricky. But if we disallow our mirror to change the energy of the photons during the reflection, then energy conservation and some basic facts from the quantum theory of light will help (energy conservation, by the way, corresponds to a symmetry as well, this symmetry is time translation). If we supposedly know that $E = \hbar k = \hbar \sqrt{k_x^2 + k_y^2 + k_z^2}$, then $E = E'$ and the fact that $k_x$ and $k_z$ do not change, constrains the reflection to the observed behaviour $k_y' = -k_y$. (Note that this energy conservation argument can also be made rigorous for a classical wave packet. In that case the formulation will, however, be much more complicated).
Sebastian Riese
- 13,484
- 2
- 44
- 64
0
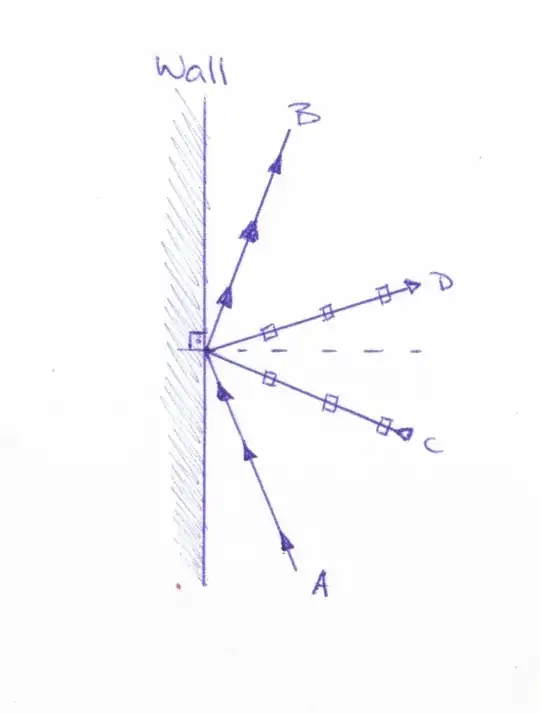
Imagine you throw a tennis ball at a wall. If you throw it perpendicular to the wall, it'll bounce right back, but if you bounce it at an angle, it will bounce exactly in the "opposite" direction (without taking friction and elasticity into account). If you are located at A and throw the ball, it will bounce off to B. If you're at C and throw it, it'll go to D. The same applies to light: if you shine a light at an angle from A, the light will reflect and go to B and so on.
Just to clarify, I say "opposite" because it is not called opposite. But I understand what you mean :)
Pablowako
- 132
- 12