5

Consider a sphere of radius $R$ & density $\rho_s$, falling through a liquid having density $\rho_l$, attains a constant terminal velocity $V_t$ then in this case the net force acting on the sphere is zero. Neglecting effect of buoyancy (see in the picture below),
$$F_{\text{net}}=F_{d}-F_{\text{g}}=0\iff F_d=F_g$$ $$6\pi\eta r V_t=\frac{4}{3}\pi r^3 \rho_s g$$ $$V_t=\frac{2}{9}\frac{gr^2\rho_s}{\eta}\tag 1$$

enter image description here

But, viscous drag force is also given as $F_d=\frac{1}{2}C_dA\rho_lV_t^2$ hence, $$\frac{1}{2}C_dA\rho_lV_t^2=\frac{4}{3}\pi r^3 \rho_s g$$ for sphere, setting $C_d=\frac{1}{2}$ & $A=\pi r^2$ $$\frac{1}{2}\frac{1}{2}\pi r^2\rho_lV_t^2=\frac{4}{3}\pi r^3 \rho_s g$$ $$V_t=4\sqrt{\frac{rg\rho_s }{3\rho_l}}\tag 2$$ The question is: do (1) & (2) give the same terminal velocities ($V_t$) if not then which one is correct ?

Any help will be appreciated. Thanks

Harish Chandra Rajpoot
  • 2,517
  • 22
  • 25
  • 41

3 Answers3

4

The drag coefficient $C_D$ is not constant for a sphere - setting it equal to 0.5 is a convenient shortcut. The actual relationship is complex, as demonstrated by the following plot (from http://www.wikiwand.com/en/Drag_coefficient)

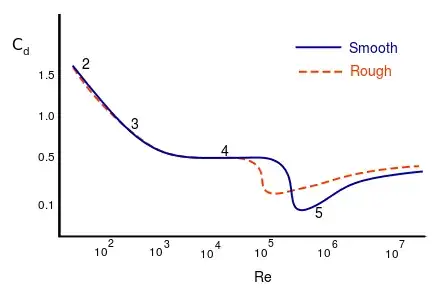
enter image description here

This shows the drag coefficient varies quite a lot with Reynolds number, which itself is given by

$\rm{Re}=\frac{\rho v \ell}{\mu}$$

Where $\rho$ is the density, $v$ the velocity, $\ell$ a "typical length scale" (the diameter in case of a sphere) and $\mu$ the dynamic viscosity.

As you can see, $\rm{Re}$ is a function of $v$ - so there may not be a closed form solution. Instead you might start with the quadratic drag expression, assume a $C_D$ of 0.5, and compute $v$. You then calculate $\rm{Re}$, use it to get a better estimate for $C_D$, and repeat... If you end up at very small Reynolds numbers you may want to try the linear (Stokes) drag instead - there is no well defined transition between the two equations.

The key point is this: the laminar (Stokes) equation is only valid for very small Re: so if you end up calculating a terminal velocity where Re is not so small, then you should probably repeat the calculation with the quadratic expression. Only when the result is self-consistent do you know you have done it right.

So yes - the two expressions are both valid (in their own way) and they give different results. Caution is needed - but in general very small particles tend to have laminar flow and follow Stokes' law, while big ones are turbulent. The exact transition between the two is not easy to define.

You may find it instructive to try to plot the terminal velocity for a particle by changing its density and thus the force - and to do so for both equations. It would require you to create a lookup table for the drag coefficient but it's an exercise that would give you more insight into this kind of behavior than you would get if I just did the work for you.

Community
  • 1
Floris
  • 119,981
2

Yes, both the formula (1) & (2) are equally applicable under certain conditions.

Formula (1) is valid for small bodies over which the flow is usually laminar

while formula (2) gives terminal velocity for both large bodies over which flow is turbulent.

Hope it helps

0

Equation (1) is even more restrictive than laminar, it is for so-called creeping flow which is with a Re near zero. Full turbulent flow does not occur until the discontinuity you see in the plot around the point labelled 5 on the plot. Equation (1) is valid in the initial linear region. From your plot, form about Re=0 to about point 3. As others have mentioned, Cd is also not a constant. In the creeping flow regime it is 24/Re.

Dr. Dr. Paul E Crittenden
  • 1
  • 1