Interpretation of QED gauge freedom

Question

In quantum (or classical) electrodynamics we are free to make gauge transformations, which change the form of terms in the Feynman diagrams (or the potentials) without affecting any physical observable. This is sometimes viewed as a flaw in the theory.

A similar freedom exists in general relativity. However, here the gauge freedom admits a compelling physical interpretation: it reflects our freedom to describe events using arbitrary coordinates; i.e. the independence of physics from the marks we choose to put on our rulers.

Is there a similarly physical way of interpreting the QED gauge freedom?

Answer 1

Yes, there is. When you adjust the gauge you change the phase.

Thus the difference in phase between two points can basically be anything you want, just adjust the phase and compensate the gauge, or adjust the gauge and compensate the phase.

Answer 2

There is no "physical" interpretation of internal gauge symmetries. Gauge symmetries are reflections of an overcounting of degrees of freedom¹, or, equivalently, of the presence of constraints. While the gauge principle is a powerful theoretical tool, the symmetry itself is not really "physical".

General relativity is a special case - and not a "proper" gauge field theory - because diffeomorphisms of spacetime (which you may view as mere "coordinate changes", but which you may also consider active transformations like actual rotation) naturally induce gauge transformations by the Jacobian: The Jacobian is a "local $\mathrm{GL}(n)$ gauge transformation", if you wish. This gauge symmetry is not internal, it interacts with the parameters (the spacetime coordinates/manifold) of the theory, not merely with aspects of its degrees of freedom (the fields living on the manifold). Hence general relativity gets a "physical" interpretation because the "gauge" transformations are not decoupled from the "physical" choice of coordinates.

"Proper" gauge field theories don't do that. They live "above" spacetime, and whatever you do on spacetime has no gauge-theoretic effect whatsoever. They purely act on the fields, and even there only on those that carry a gauge charge - which is essentially the marker for them containing redundant information, which is nevertheless kept to achieve a more elegant formulation, in particular keep (some other) manifest symmetry or avoid having to deal with locally solving the constraints and running into the Gribov problem as long as possible.²

To say that the $\mathrm{U}(1)$ gauge of quantum electrodynamics "adjusts that phase" is correct - but it is not a physical interpretation! An overall (even local) phase is unphysical to begin with, only relative phases play a role, that is the whole reason we are allowed to make a proper gauge theory out of this. Quantum theories don't care for phases, quantum states are rays in Hilbert spaces - using individual vectors in a Hilbert space is already an overcounting of degrees of freedom, paving the way to have a gauge theory in the "second quantized" description.

---

^{1See also Gauge symmetry is not a symmetry?}

^{2This might be the "flaw" your professor alluded to - the quantization of gauge theories is much more difficult than that of unconstrained theories (because their Hamiltonian formulation is much more complicated) and may even fail non-perturbatively in some cases. However, they are the only known way (well, known to me, granted) to express things like the strong and weak force in a way amenable at all to quantization.}

Answer 3

In quantum (or classical) electrodynamics we are free to make gauge transformations, which change the form of terms in the Feynmann diagrams (or the potentials) without affecting any physical observable. This is sometimes viewed as a flaw in the theory.

I've not heard anybody else say that. Can you give a reference?

A similar freedom exists in general relativity. However, here the gauge freedom admits a compelling physical interpretation: it reflects our freedom to describe events using arbitrary coordinates; i.e. the independence of physics from the marks we choose to put on our rulers.

Yes. What happens happens, regardless of your state of motion. Your state of motion is usually why you adopt a particular coordinate system. If you're sitting in your chair at home you typically think of yourself as motionless: you disregard the rotation of the Earth, and you use a paper map as the basis of your coordinate system. If you're a lunar astronaut you disregard the Earth's orbital motion around the Sun, but your charts accommodate the Moon's orbit around the Earth, and the Earth's daily rotation too. But whatever your map/chart/coordinate system, the events that happen out there happen regardless of the coordinate system you use, and regardless of how you're moving.

Is there a similarly physical way of interpreting the QED gauge freedom?

Yes. See the Wikipedia Gauge Fixing article? I imagine most people will tell you it's reasonable, and it matches their understanding. But see how it refers to electric field E and magnetic field B? Well, guess what? There are no such fields. See section 11.10 of Jackson's Classical Electrodynamics where he said "one should properly speak of the electromagnetic field F_μν rather than E or B separately". That's because E and B denote the linear and rotational forces that result from electromagnetic field interactions. If you're a positively-charged particle and I set you down near a motionless electron, you experience a linear force, and you might claim that the electron has an electric field E. If however I were to throw you past that electron, you also experience a rotational force, and you might claim that the electron also has a magnetic field B. However your motion did not change the electron's field, not one jot. Both you and that electron have an electromagnetic field, and the electromagnetic field has a dynamical "spinor" nature, not altogether unlike the gravitomagnetic field. The linear and rotational forces that result from electromagnetic field interactions are not actually fields. That's why Minkowski said this in Space and Time:

"In the description of the field caused by the electron itself, then it will appear that the division of the field into electric and magnetic forces is a relative one with respect to the time-axis assumed; the two forces considered together can most vividly be described by a certain analogy to the force-screw in mechanics; the analogy is, however, imperfect".

Sadly this "unification" aspect of electromagnetism seems to be absent from Gauge transformation. I find it rather odd myself. Take a look further down the Wikipedia article Gauge Fixing and you can see this:

"Not until the advent of quantum field theory could it be said that the potentials themselves are part of the physical configuration of a system. The earliest consequence to be accurately predicted and experimentally verified was the Aharonov–Bohm effect, which has no classical counterpart".

I know it's only Wikipedia, but IMHO by and large it accurately represents the views of many physicists. But if you know anything about gravity, you will surely bridle at the idea that potentials aren't real. And if you know anything about classical electromagnetism you will surely bridle at the Wikipedia Aharonov-Bohm banging on about the electromagnetic fields E and B. Especially if you know about Ehrenberg and Siday's Refractive Index in Electron Optics and the Principles of Dynamic:

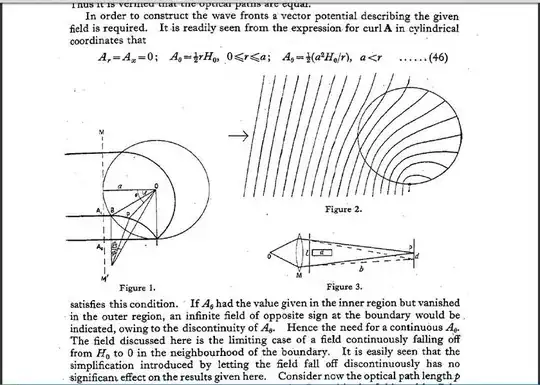
This is the semi-classical paper dating from 1949 that predicted what's now known as the Aharonov-Bohm effect. All in all, when you turn over this rock, what you find is a can of worms.