If I know the positions and the speeds of each particle in a box over the time, how can I compute the entropy ?
(I`m making a simulation where I want to show that the disperion of the particles over the time increases the entropy.)
preview :
nb: it`s not a shower, particles are free, they are not falling...
video:
http://www.legtux.org/?page=upload&id=6184777976
code :
the code will be released when ready with some videos of real experimentations made. We have differents situations to program, not only the present one.
entropy:
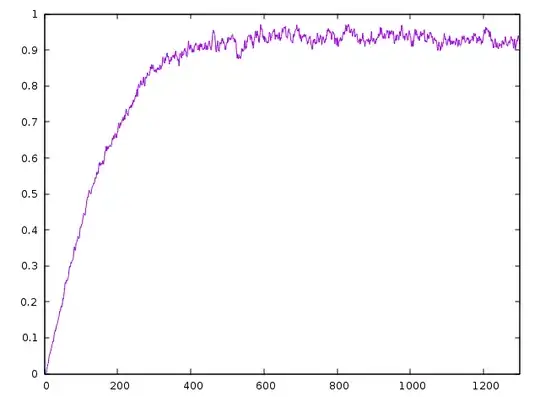
on the suggestion of qftishard I computed the entropy of the simulation presents in the video,
$$S = - k_\mathrm{B} \sum p_i \ln p_i $$
(Gibbs Entropy Formula ?)
nb1: I didn't use gnuplot for years, so I don't remember how to add nice title, etc. I took this screenshot quickly...
nb2: I scaled the entropy from 0 to 1 on purpose. But of course I don`t have zero entropy at the beginning of the simulation.
- we can see that the entropy is lower when the particles are not dispersed.
- we see the maximum of entropy (with some variations) when particles are dipsersed.
- we see that the system never get back, even close, to his initial state.
- we see that the entropy is rising over time to reach a maximum, so we conclude our system respect the second law of thermodynamic.
- so, I consider this simulation succeeded! thx guys.