I'm going to assume your window has dimensions of 1x1, in length units. Since it's a video game units don't really matter. The gravity acceleration you're looking for will be a vector with 2 components.
$$\langle a_x, a_y\rangle$$
Next, I'm going to say the spaceship is at the origin with the asteroid at (x,y). This just makes it easier. The gravity from a single asteroid will be:
$$\vec{a} = \frac{\vec{r}}{\left| \vec{r} \right|^3}$$
$$a_x = \frac{-x}{ \left( x^2 + y^2 \right)^{3/2}}$$
$$a_y = \frac{-y}{ \left( x^2 + y^2 \right)^{3/2}}$$
Here again I exercised reckless disregard for units. One way to tackle your problem is to actually sum up the acceleration from an entire infinite lattice of masses that repeat every x and y increment. If you do this for the top right quadrant alone you'll simply find it diverges. A way around this is to sum the contribution from a point of index (i,j) with a point in the 3 other quadrants of indices (-i,j), (i,-j), and (-i,-j). That series will converge for the calculated acceleration but not the potential. Here is a formalism of what I've described.
$$x_{i} = x+i$$
$$x_{-i} = x-1-i$$
$$y_{j} = y+j$$
$$y_{j} = y-1-j$$
I've reserved the $i=0$ and $j=0$ values for the 4 asteroids closest to the origin. Now we can write the acceleration from a given set of 4 asteroids with one (i,j) index pair.
$$a_{xij} = \frac{-x_{i}}{(x_{i}^2+y_{j}^2)^{3/2}} - \frac{x_{-i}}{(x_{-i}^2+y_{j}^2)^{3/2}} - \frac{x_{i}}{(x_{i}^2+y_{-j}^2)^{3/2}} - \frac{x_{-i}}{(x_{-i}^2+y_{-j}^2)^{3/2}}$$
$$a_{yij} = \frac{-y_{j}}{(x_{i}^2+y_{j}^2)^{3/2}} - \frac{y_{j}}{(x_{-i}^2+y_{j}^2)^{3/2}} - \frac{y_{-j}}{(x_{i}^2+y_{-j}^2)^{3/2}} - \frac{y_{-j}}{(x_{-i}^2+y_{-j}^2)^{3/2}}$$
Then we can just take these contributions and do a double infinite sum.
$$a_x = \sum_{j=0}^{\infty} \sum_{i=0}^{\infty} a_{xij}$$
$$a_y = \sum_{j=0}^{\infty} \sum_{i=0}^{ \infty} a_{yij}$$
We're basically finished here. I thought it would be easy to get a closed form solution for the series, but it really isn't. I did implement it numerically. Note that your calculations grow as $n^2$ where $n$ is the upper limit of your series because it's a double sum. I found that $n=0$ gives an error about 5% and drops rather slowly for higher values. When making your code, you'll need to consult a mathematician or apply some set of tricks in order to a smoothly behaving code. You'll probably find it easiest to calculate a vector field that has good accuracy and then just interpolate values from that when running the code. However, that's only for points far from the asteroid. Once you get very close to the asteroid this method will break down and you'll want to use an integration technique that can handle the large slope in that region. Thankfully, the contribution from the asteroid mirror images will diminish as you get close to it, and you can transition to a single $1/r^2$ acceleration.
Addition:
There seems to be some skepticism as to whether or not the series should converge at all. I assure you it does. Below are the x and y components ($\langle a_x, a_y\rangle$) of the acceleration computed with the method described here, doing a sum to $5$. That means, $5^2=25$ terms in the series sum with 4 asteroids for each term, resulting in 100 total asteroids. So the following is the acceleration from a mesh of 100 asteroids in a 10x10 mesh around the origin. You can increase the side form 10 to 400 asteroids and you only get a small revision in these numbers.
x-component
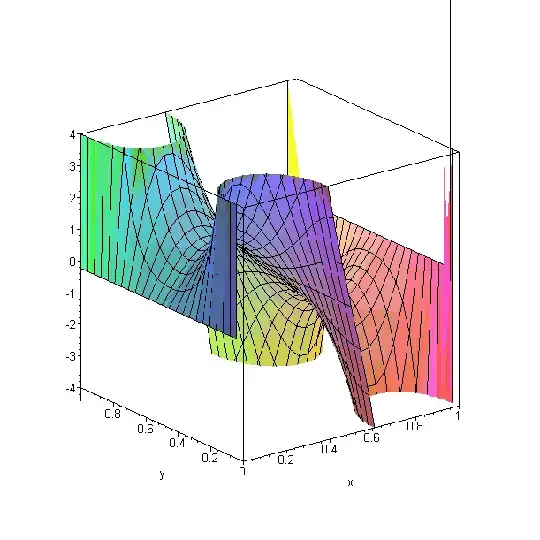
y-component
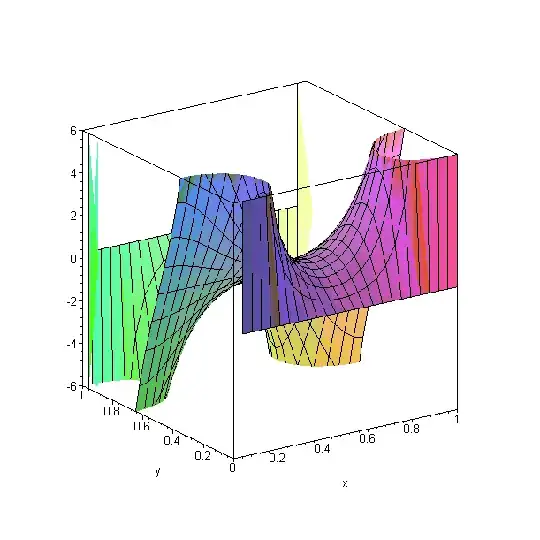
This is smooth, continuous, and repeating, exactly as expected. To a very good level of accuracy, this is the field from an infinite mesh of asteroids doing a $1/r^2$ sum as described above. It does converge.

