Angular momentum about a moving axis

Question

How can we define angular momentum of a system about an axis that moves parallel to itself? For example Axis passing through CM that is perpendicular to plane of body.

When we talk about conservation of momentum, then does it mean that angular momentum about a particular fixed axis remains same, or can we prove this for an axis that moves parallel too?

For example if a disk is falling freely. Can we say that Angular Momentum about an axis passing through CM and perpendicular to disk will remain same? How can we say this?

Answer 1

Angular momentum is a vector defined by $$\vec{L}_{cm} = I_{cm} \vec{\omega}$$ where $I_{cm}$ is a 3×3 mass moment of inertia about the center of mass. When the rotational velocity vector $\omega$ is about one of the principal inertial axes then the angular momentum vector is parallel to the motion axis and $\vec{L}_{cm} =m \rho^2 \vec{\omega}$ where $m$ is the scalar mass, and $\rho$ is the scalar radius of gyration about that axis.

If a body is not rotating with $\vec{\omega}=\vec{0}$ then it will have no angular momentum (It may still have linear momentum $\vec{p} = m \vec{v}_{cm}$).

I really do not understand your question, as we do not decide what axis do define angular momentum about. It comes out from the motion and inertial properties of the body. Conservation of angular momentum states that when the net torques about the center of mass is zero, angular momentum vector does not change.

It is a consequence of the law of rotational motion.

$$ \sum \vec{\tau}_{cm} = \frac{{\rm d}}{{\rm d}t} \vec{L}_{cm} $$

Additionally, to define angular momentum about any other point A, let say located $\vec{r}_A$ away from the center of mass you have to consider the moment of linear momentum also

$$ \vec{L}_A = \vec{L}_{cm} - \vec{r}_A \times \vec{p} $$

Since linear velocity transforms in a similar way

$$\vec{v}_A = \vec{v}_{cm} - \vec{r}_A \times \vec{\omega} $$

you can establish the momentum vectors about any arbitrary point A as a function of the motion of this point

$$ \begin{align} \vec{p} & = m ( \vec{v}_A + \vec{r}_A \times \vec{\omega} )\\ \vec{L}_A & = I_{cm} \vec{\omega} - \vec{r}_A \times \vec{p} \end{align}$$

This is important because it is used to establish the equations of motion for rigid bodies about points away from the center of mass. See this answer (Derivation of Newton-Euler equations of motion) for more details.

Answer 2

The angular momentum $L$ of an object is always defined with regards to the axis about which rotation takes place:

$$L=I\omega,$$

where $I$ is the inertial moment and $\omega$ the angular speed.

The inertial moment is defined and can be calculated as shown here. Where it's necessary to calculate $I$ with respect to another axis parallel to the first one, the Parallel Axis Theorem can be used.

Now with regards to angular momentum, analogous to linear momentum, it is a conserved quantity. In order to change linear momentum a force needs to be applied and in order to change angular momentum a torque (moment, couple [syn.]) needs to be applied.

How can we define angular momentum of a system about an axis that moves parallel to itself? For example Axis passing through CM that is perpendicular to plane of body.

I'm not sure I understand your question correctly. Angular momentum is always defined about an axis of rotation. If that axis itself moves the object will have both angular momentum $I\omega$ AND linear momentum $mv$ ($v$ is linear speed of that axis).

Look at the diagram below:

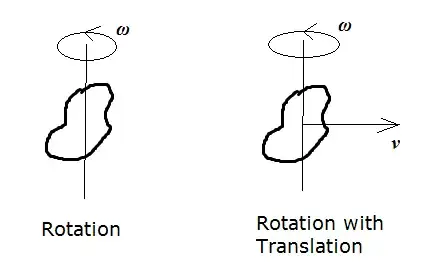
Left, the object rotates about an axis at constant $\omega$: pure rotation.

Right, the object rotates about an axis at constant $\omega$ and the axis moves parallel to itself at speed $v$: we have rotation and translation happening at once.

In both cases the angular momentum is exactly the same but the right object has linear momentum too.

The total kinetic energy of the object would be $K$:

$$K=\frac{I\omega^2}{2}+\frac{mv^2}{2}.$$

When we talk about conservation of momentum, then does it mean that angular momentum about a particular fixed axis remains same, or can we prove this for an axis that moves parallel too?

Yes. Even if that axis moves the angular momentum is conserved, until some torque acts on the object to alter its angular speed $\omega$.

An example is a cylinder rolling down a smooth slope: provided there's enough friction both angular and linear momentum will change because friction provides the couple $\sigma$ to alter $\omega$.

For example if a disk is falling freely. Can we say that Angular Momentum about an axis passing through CM and perpendicular to disk will remain same? How can we say this?

As long as no couple acts on the rotating disc, its angular speed and thus its angular momentum $L=I\omega$ will not change.