The Dual Cloud Chamber Paradox

Question

2012-04-07 Addendum: The Dual Cloud Chamber Paradox

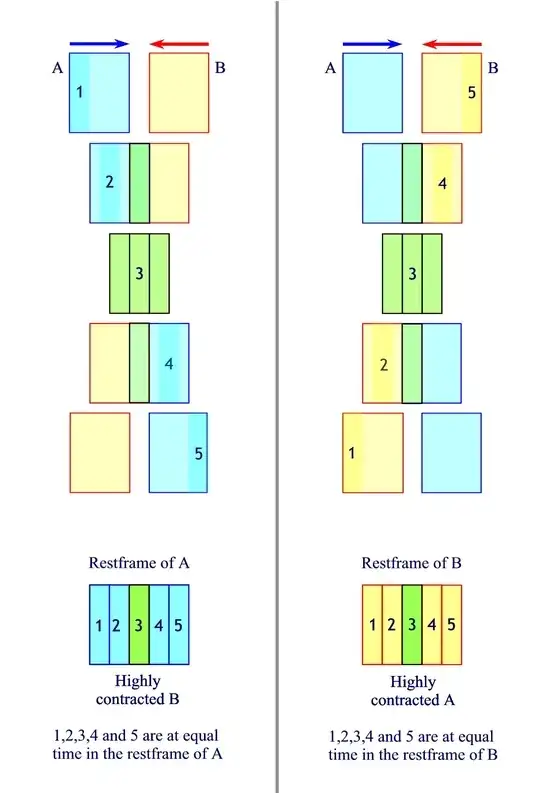
Two 10m diameter spheres $A$ and $B$ of very cold, thin gas have average atomic separations of 1nm. Their atoms are neutral, but ionize easily and re-radiate if a relativistic ion passes nearby. Both clouds are seeded with small numbers of positive and negative ions. The clouds collide at a relative speed of $0.994987437c$, or $\gamma=10$. Both are sparse enough to minimize collisions and deceleration. Both show passage of each other's ions. (a) What do distant observers moving parallel to $A$ and $B$ observe during the collision? (b) Are their recordings of this event causally consistent?

The answer to (a) requires only straightforward special relativity, applied from two perspectives. For the traveler moving in parallel to cloud $A$, cloud $B$ should appear as a Lorentz contracted oblate spheroid with one tenth the thickness of cloud $A$, passing through cloud $A$ from right to left. If you sprinkled cloud $A$ with tiny, Einstein-synchronized broadcasting clocks, the $A$-parallel observer would observe a time-stamped and essentially tape-recording like passage of the $B$ spheroid through cloud $A$.

The $B$-parallel observer sees the same sort of scenario, except with cloud $A$ compressed and passing left-to-right through cloud $B$. If $B$ is sprinkled with its own set of Einstein synchronized broadcasting clocks, the $B$p-parallel observer will record a time-stamped passage of the compressed $A$ through $B$.

So, am I the only one finds an a priori assumption causal self-consistency between these two views difficult to accept? That is, while it may very well be that a recording of a flattened $B$ passing through cloud $A$ in $A$-sequential time order can always be made causally self-consistent with a recording of a flattened $A$ passing passing through through cloud $B$ in $B$-sequential order, this to me is a case where a mathematically precise proof of the information relationships between the two views would be seem like a good idea, if only to verify how it works. Both views after all record the same event, in the sense that every time a clock in $A$ or $B$ ticks and broadcasts its results, that result becomes part of history and can no longer be reversed or modified.

It's tempting to wonder whether the Lampa-Terrell-Penrose Effect might be relevant. However, everything I've seen about L-T-P (e.g. see the video link I just gave) describes it as an optical effect in which the spheres are Lorentz contracted at the physical level. Since my question deals with fine-grained, contact-like interactions of two relativistic spheres, rather than optical effects at a distance, I can't easily see how L-T-P would apply. Even if it did, I don't see what it would mean.

So, my real question is (b): Does an information-level proof exist (not just the Lorentz transforms; that part is straightforward) that the $A$-parallel and $B$-parallel recordings of dual cloud chamber collision events will always be causally consistent?

---

2012-03-03: This was my original version of the question, using muonium clocks

My SR question is how to predict length contraction and time dilation outcomes for two interacting beams of neutral particles. The two beams are:

1. In different inertial (unaccelerated) reference frames for the duration of measurement part of the experiment.

2. Intermixed at a near-atomic level so that frame-to-frame photon exchange times are negligible. An example would be two intersecting beams of relatively dense, internally cold muonium atoms.

3. Clock-like even at the atomic level (e.g., decaying atoms of muonium).

4. Part of a single causal unit. By this I mean that there is a sufficient short-range exchange of photons between the two beams to ensure that state changes within each beam have an entropic effect, however small, on nearby components of the other beam. This makes their interactions irreversible in large-scale time. An example would be decay of an anti-muon in one frame transferring energy to nearby muonium atoms in the other frame. Simply illuminating the intersection region with light frequencies that would interact with muonium in both of the beams would be another option.

5. Observed by someone who is herself isolated from the rest of the external universe.

Muons generated by cosmic rays and traveling through earth's atmosphere provide a helpful approximation the above experiment. The muons provide the first beam, and the atmosphere forms the second one, which in the case of muons is shared by the observer.

Such muons have tremendously extended lifespans, which is explained by invoking time dilation (but not length contraction) for the muon frame as viewed from the atmosphere frame. Conversely, length contraction (but not time dilation) is invoked to describe the view of the atmosphere from the perspective of the muon frame. Since this results in the atmosphere appears greatly compressed in the direction of travel, the muons simply travel a shorter distance, thereby ensuring the same decay result (causal symmetry) for both views of the interacting frames.

My question then is this:

For the thought experiment of intersecting, causally linked beams of muonium, what parameters must the observer take into account in order to predict accurately which of the two intersecting muonium beams will exhibit time dilation, and which one will exhibit length contraction?

2012-03-04 Addendum by Terry Bollinger (moved here from comment section):

Sometimes asking a question carefully is a good way to clarify one's thinking on it. So, I would now like to add a hypothesis provoked by own question. I'll call it the local observer hypothesis: Both beams will be time dilated based only on their velocities relative to the observer Alice; the beam velocities relative to each other are irrelevant. Only this seems consistent with known physics. However, it also implies one can create a controllable time dilation ratio between two beams. I was trying to avoid that. So my second question: Are physical time dilation ratios ever acceptable in SR?

2012-03-06 Addendum by Terry Bollinger:

Some further analysis of my own thought problem:

A $\phi$ set is a local collection of clock-like particles (e.g. muons or muonium) that share a closely similar average velocity, and which have the ability to intermix and exchange data with other $\phi$ sets at near-atomic levels, without undergoing significant acceleration. A causal unit $\chi = \{\phi_0 ... \phi_n\}$ is a local collection of $(n+1)$ such $\phi$ sets. By definition $\phi_0$ contains a primary observer Alice, labeled $\aleph_0$, where $\aleph_0 \subset \phi_0$.

Each $\phi_i$ has an associated XYZ velocity vector $\boldsymbol{v_i} = (\phi_0 \rightarrow \phi_i$) that is defined by the direction and rate of divergence of an initially (nominally) co-located pair of $\phi_0$ and $\phi_i$ particles, with the $\phi_0$ particle interpreted as the origin. The vector has an associated magnitude (scalar speed) of $s_i=|\boldsymbol{v_i}|$.

Theorem: If $\phi_i$ includes a subset of particles $\aleph_i$ capable of observing Alice in $\phi_0$, then $\aleph_i$ will observe $\phi_0$ as length contracted along the axis defined by $\boldsymbol{v_i}$. Conversely, Alice ($\aleph_0$) will observe each $\phi_i$ as time dilated (slowed) based only on its scalar speed $s_i$, without regard to the vector direction. This dependence of time dilation on the scalar $s_i$ means that if $\phi_a$ has velocity $\boldsymbol{v_a}$ and $\phi_b$ has the opposite velocity $\boldsymbol{-v_a}$, both will have the same absolute time dilation within the causal unit (think for example of particle accelerators).

Analysis: This $\chi = \{\phi_i\}$ framework appears to be at least superficially consistent with data from sources such as particle accelerators, where time dilation is observable in the variable lifetimes of particles at different velocities, and where absolute symmetry in all XYZ directions is most certainly observed. Applying observer-relative time dilation to fast particles (e.g. in a simple cloud chamber) is in fact such a commonly accepted practice that I will assume for now that it must be valid.

(It is worth noting that while particle length contraction is typically also assumed to apply to fast-moving particles, serious application of length contraction in a causal unit would cause the particles to see longer travel paths that would shorten their lifespans. This is the same reason why muons are assumed to see a shorter path through a length-contracted atmosphere in order to reach the ground.)

My updated questions are now:

(1) Is my $\chi = \{\phi_i\}$ framework for applying SR to experiments valid? If not, why not?

(2) If $\chi = \{\phi_i\}$ is valid, what property makes the observer $\aleph_0$ in $\phi_0$ unique from all other $\aleph_i$?

Answer 1

Have a look at the images below. Both sides show cloud A moving through cloud B as you would expect. Now at the left side we are going to collect 5 slices which are at equal time in the restframe of A, and at the right side we collect 5 slices which are at equal time in the restframe of B. This corresponds with the rotation of the time axis in these two reference frames.

As you can see, the left image shows a highly contracted cloud B inside the cloud A while the right image shows a highly contracted cloud A inside cloud B, exactly as you describe. Now note that both are part of the same 4D reality. What you see are two different 3D spaces cut out of the same 4D space-time.

Hans

Answer 2

Naturally there's no "universal" time in the SR, the time difference of two events may be different in different reference frames, and in particular it may be negative (i.e. order of the events may be different as well).

However there are two distinct things:

1. The time of the event, according to a specific reference frame's coordinate + time system.
2. The time at which an observer in a particular reference frame receives the information about the event.

As you probably know, there's a maximal speed at which the information may be passed according to SR, which is the speed of light in vacuum (or any other particles with no rest mass). Hence an observer in a particular reference frame does not register an event the same moment it occurs in its reference frame. There's a delay, which depends on the distance between the event and the observer (in the context of its reference frame). So, when you talk about two events that occur at different locations - this should be taken into account to realize what the observer actually "sees".

Accounting for this one resolves all the causality-related paradoxes, such as a "ladder paradox".

More information here. See "Causality and prohibition of motion faster than light"

Answer 3

I'll make an argument intended to make the Lorentz transformation more natural. The reason this seems so odd is because you're thinking about it from the point of view of matter. This is a natural thing to do because people are made out of matter. But Einstein's work is much simpler if you think about things from the point of view of light. With light, the natural speed is always $c$. And there's an argument in favor of treating matter as if its natural speed were also $c$. If you follow that argument, then the Lorentz transformations follow.

The Standard Model of elementary particles represents the fermions (matter) as chiral fields. These are a Dirac field (which can model, for example, the combination fields of electron and positron) which are split into "chiral" or "handed" halves. These left and right handed fields are a little familiar to undergraduate physics as their equivalents appear when light is circularly polarized into left or right handed light.

To turn an electron into a pure right handed or left handed field, one accelerates the electron in the direction of its spin (or the opposite direction) to the speed of light. This is of course impossible except in the limit. But the underlying notion is clear, the Standard Model is built from components that naturally travel at light speed.

So your intuition will understand the situation better if you think of matter as being the weird and bizarrely behaved stuff. Light acts perfectly normally, just what you'd expect of waves in a universe where the wave speed is $c$.

If you look at the problem this way, you will see that the transformation of the pictures from one clump to the other involves a great deal of complexity. You have to arrange for matter to do some pretty crazy things in order to get all those "stationary" clocks.

On the other hand, if you think of the problem as one where fields that travel at a natural speed of $c$ interact, then one naturally chooses a single reference frame and carries out all calculations in that frame of reference. Of course, since we are made out of fields that move at speed $c$, we cannot detect that reference frame. Since we cannot detect it, it is not "preferred" by our laws of physics. We could just as easily have chosen the "wrong" rest frame, our calculation would give the same result either way because waves can measure absolute wave speeds or absolute wave frequencies or absolute wave lengths; they can only measure differences and the results are the laws of Lorentz transform.

As an example, suppose you are a small localized wave. You cannot know your absolute speed against the background (say water for instance, though this is not a good example). When another wave comes by, all you can do is say what their wavelength is compared to your own wavelength. But your own wavelength gets changed when you are in fast moving water. That's because the time that a wave saves going downstream (with the current) is less than the time it loses going upstream.

Suppose the speed of your waves is $c$, and you need to travel some distance $l$. The time required to go there and back will be $t = l/c+ l/c = 2l/c$. Now suppose that there is a current at speed $v$. This will speed you up one way and slow you down the other. So the time required becomes: $$t = l/(c+v) + l/(c-v) = \frac{l(c-v)}{(c+v)(c-v)} + \frac{l(c+v)}{(c+v)(c-v)}$$ $$= \frac{2cl}{c^2-v^2} = \frac{2l}{c}\frac{1}{1-v^2/c^2}\;\;\textrm{so}$$ $$t = \frac{2l}{c}\gamma^2$$ where $\gamma = (1-v^2/c^2)^{-1/2}$ is the usual relativistic gamma factor. Looked at relativistically, you can rearrange the calculation to be $(t/\gamma) = 2(l\gamma)/c$. To get the old result $t=2l/c$, you have to apply two changes. You apply length contraction so that $l\to l/\gamma$ and time dilation so that $t\to t\gamma$. Thus the Lorentz transformation is natural for beings made of waves, living in a universe of waves, who can use only waves to measure.

---

So much for why it is that Lorentz transformations are natural. Now as to why causality can have different rest frames. If you accept that everything must be made out of waves, then the wave speed itself gives a limit to causality. Nothing can happen before a wave gets there. So you are free to choose a reference frame so long as your reference frame is slower than light it cannot a violation of causality. (Because casusality uses waves.)

Answer 4

In my answer I will use the known properties of the light. The light propagates isotropically wrt the medium irrespective of the speeds of the source and of the receiver and has a constant value if measured by a non-accelerating observer. The source is Einstein (I.1.2 §2 of 1905 paper) :

Every ray of light moves in the "stationary" co-ordinate system with the definite velocity V, the velocity being independent of the condition, whether this ray of light is emitted by a body at rest or in motion

The other source is the online book of Hans de Vries where relativity is very well explained and where we can see (chapter 4, I think) that there exists a real length Lorentz contraction and not only an apparent one. The other source is the pos-Einstein paper Cosmological Principle and Relativity - Part I (arxiv) (is poison..;)

...generalizing Relativity Principle to position... .., and analysed the space-time structure. Special Relativity space-time is obtained, with no formal conflict with Einstein analysis, but fully solving apparent paradoxes and conceptual difficulties, including the simultaneity concept and the long discussed Sagnac effect. ...

I dont see any problem in causality and I've done a nice image (my 1st in Inkscape) to show how I see the problem. If you think that this is a paradox to the relativistic guys then you should also see PSE - Twin paradox - observers counter orbiting pose a serious problem to the relativistic minds (only those that can only think with an equation in front of the eyes).