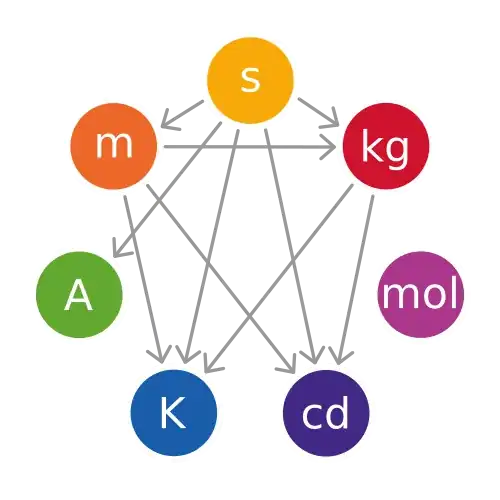
So a unit provides two different things: type and scale. When you say e.g. $1000 \text{ ms} = 1\text{ s}$ you are communicating both a type-equality and a scale factor between them.
Type, in physics, is really subtle. Yes, we can make do with a lot fewer types than the SI system uses; in fact physicists using Planck units frequently make do with only one type (though this depends on the fact that they don't have a unit for luminous intensity and use 1 as their unit of numbers-of-particles). Similarly, some programming languages are very weakly typed; for example with shell scripting you mostly have to think "everything is a string" to survive.
At the same time, we routinely make type-level judgments which exist at a higher level than the SI units. One super-simple example is that the SI system does not encode a type difference between an integer, an angle, and a solid angle, but most people will conceptually separate these and, for example, if one is talking about the solid angle subtended by a penny at arm's length, one would tend to refuse to add the integer 2 to it. Another simple example: many (most?) physicists have been burned at one point or another by a confusion between frequencies and angular velocities; these have the same SI type of $T^{-1}$ and are separated by a scale of $2\pi$: but frequently this difference is just enough to accidentally misconfigure a calculation or experimental apparatus to the point of "it's not working, and it should be! Why is this result 0 instead of the peak that I was looking for?!" ... so you learn to keep a mental type classification between angular frequencies $\text{rad/s}$ and absolute frequencies $\text{Hz}$ (or however you want to think of them).
(In fact this mental classification is so rigid that even though the Fourier transform convention $$g[f] = \underset{t\to f}{\mathcal F} ~~g = \int_{-\infty}^{\infty} dt~e^{-2\pi \mathrm i~f~t}~g(t)$$is in many ways superior (it has no normalization factors and gives you the absolute frequencies rather than angular ones), it is much more common in physics to see $e^{-i~\omega~t}.$ That this should be negative is a separate matter best exemplified by the Dirac $\delta$-function.)
The SI base units are therefore not an exhaustive list of types; rather, the SI type system is simplified from the much more rich type system in physicists' heads, to a plainer model which is the span of those base units' types. This makes it much easier, for example, to program into a computer. For example in Haskell, which is strictly typed, you could program it to do runtime type checking as:
import Data.Ratio -- rational numbers
type Q = Ratio
-- define the type-level data structure as an object with 7 rationals describing the
-- exponents of the different type-dimensions.
data SIType = SIType {
sit_m :: Q, sit_s :: Q, sit_kg :: Q, sit_K :: Q, sit_A :: Q, sit_mol :: Q, sit_cd :: Q}
deriving (Eq, Show)
-- define the dimensionless type
si_dimless = SIType 0 0 0 0 0 0 0
-- merge types by adding exponents termwise
mergeSITypes :: SIType -> SIType -> SIType
mergeSITypes (SIType m1 s1 kg1 k1 a1 mol1 cd1) (SIType m2 s2 kg2 k2 a2 mol2 cd2)
= SIType (m1 + m2) (s1 + s2) (kg1 + kg2) (k1 + k2) (a1 + a2) (mol1 + mol2) (cd1 + cd2)
-- actual numbers with an SI unit attached
data SI x = SI SIType x deriving (Eq, Functor, Show)
-- simple multiplication and addition
instance (Num x) => Num (SI x) where
SI t1 x1 + SI t2 x2
| t1 /= t2 = error $ "Type mismatch: saw " ++ show t1 ++ " and " ++ show t2
| otherwise = SI t1 (x1 + x2)
SI t1 x1 * SI t2 x2 = SI (mergeSITypes t1 t2) (x1 * x2)
fromInteger n = SI si_dimless (fromInteger n)
-- fmap comes from Functor above and just applies the function to the wrapped number.
negate = fmap negate
abs = fmap abs
signum = fmap signum
Since Haskell is statically typed you can also do this with compile-time checking (the essential trick is called "phantom types"), but that requires more effort, as you need to write (in principle) code for type-level rational numbers.
The SI types are independent in the sense that they represent types of physical phenomena which we would not likely confuse for each other: durations, distances, temperatures, brightnesses, masses, amounts of particles, and electric currents.
In fact the cgs systems (centimeter-gram-second) frequently use a definition of charge as "1 statcoulomb is the amount of charge $q$ such that two charges of that magnitude placed $1\text{ cm}$ away from each other experience a force of $1\text{ dyne} = 1~\text{g}~\text{cm}/\text{s}^2.$ In these systems it is very common to erase the type involved in the unit by writing e.g. $\vec F = q_1 q_2 \hat r / r^2$ and establishing essentially that $1\text{ statC} = 1\text{ g}^{1/2}~\text{cm}^{3/2}~\text{s}^{-1}$ when looking at the world without that type. The only abstract problem is that the Maxwell equations tend to take on different forms for different unit systems; in this case instead $\nabla \cdot \vec E = 4\pi~\rho.$