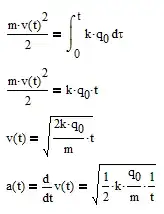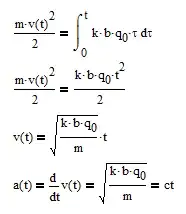Pushing down on the gas pedal of a car a good example of jerk?

Question

I'm trying to think of the clearest examples to demonstrate the concept of jerk to a layman.

Ignoring drag and making other reasonable assumptions (friction is conveniently there to only allow you to accelerate and we assume the wheels always roll without slipping), is it reasonable to say:

• A car with constant acceleration (zero jerk) would mean holding the gas pedal down at a constant displacement/angle from its starting point i.e. my foot is keeping the gas pedal held down, halfway constantly.
• A car with constant jerk (thus an increasing acceleration) would mean gradually pushing down the gas pedal so its displacement/angle is increasing from its starting point at a constant rate.

I guess what I'm asking is if jerk is proportional to the distance/angle per second that the gas pedal's position is changing at? Or is there some notable amount of jounce in there too?

Answer 1

Pushing down on the gas pedal of a car a good example of jerk? I'm trying to think of the clearest examples to demonstrate the concept of jerk to a layman.

Pushing down the gas pedal is not a good example of jerk.

A car with constant acceleration (zero jerk) would mean holding the gas pedal down at a constant displacement/angle from its starting point i.e. my foot is keeping the gas pedal held down, halfway constantly.

The answer is no (in an idealized case).

If you hold the gas pedal down at a constant angle then you inject a constant amount, $k*q_0$, of energy (mass of fuel per second multiplied with conversion constant $k$) in the car and in consequence the kinetic energy of the automobile at any moment of time, t, must be always equal to the total energy injected up to that moment t. Mathematically this can be written like this:

As you can see the solution is not a constant acceleration.

A car with ... an increasing acceleration would mean gradually pushing down the gas pedal so its displacement/angle is increasing from its starting point at a constant rate.

Again no.

If you press the pedal more and more as the time passes, at each moment you inject $q(t) = q_0*k*b*t$ where $b$ is a constant that depends on how fast you push the pedal. In consequence:

This time you get a constant acceleration.

Answer 2

Jerk in a Car

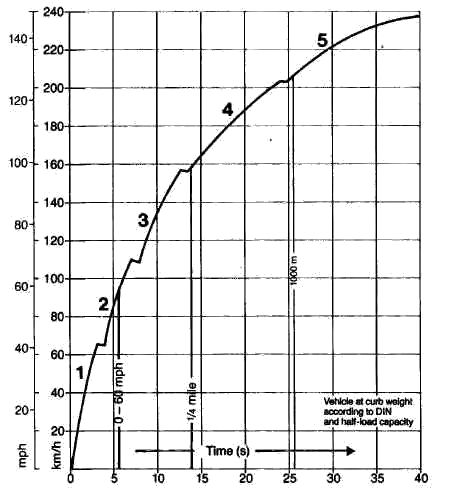
We should probably avoid talking about a car's gas pedal. Without going into too much detail, imagine when you floor it in a car. Once you've got the pedal all the way down, the car continues to accelerate, but eventually (assuming a long stretch of flat road) you will reach some steady state speed and stop accelerating. So with the pedal in a constant position, you're seeing non-constant acceleration.

If you want to stick with something familiar (I'll stay in a car), the above actually illustrates jerk fairly well: your acceleration goes from positive (non-zero) to zero. That's jerk, albeit negative jerk. Positive jerk is a bit more exciting, so let's try and look at that.

Let's assume you're driving a manual transmission car (automatic shifts will cause complications). If you're driving along at very low RPM and you push the accelerator down, you'll notice that the car accelerates, but not very quickly. This is because little power is available at low RPM. But as the car picks up speed and the RPMs increase, you eventually enter the engine's "power band" and the car will accelerate much more quickly.

Under Idealized Assumptions

I think it's worth mentioning that under your idealized gas pedal assumptions, you are correct. If the acceleration of the car is proportional to the gas pedal's angular displacement, then your second example in which you push the pedal down at a constant rate will be constant jerk with no jounce.

Jerk(s) Everywhere

I think the main problem you're running into is that you want to illustrate a practical example of jerk with no jounce. However, for real (practical) motions, this simply isn't possible. Here's a scenario that isn't terribly illuminating in a practical sense, but shows why jerk (and jounce/snap, and crackle, and pop) is unavoidable for useful motions:

1. Start with an object at rest. Velocity, acceleration, jerk, etc, are all zero and not changing with time.

2. Move the object any amount.

3. At some point in this motion, velocity was non-zero. Since velocity changed from zero to non-zero, there was non-zero acceleration.

4. Since acceleration changed from zero to non-zero, there was non-zero jerk.

5. Since jerk changed from zero to non-zero, there was non-zero jounce.

6. Continue ad infinitum (or ad nauseam, whichever comes first)

You may protest that you're object need not start from rest, but the above logic can apply starting from any change in any derivative of position. More concretely, any time you accelerate an object, you can go straight to step 3. Of course, things may no longer be changing "from zero to non-zero", but they change from their initial value to some different final value.

Answer 3

Imagine a race car starting to accelerate. You would immediately be pulled back to your seat, meaning that there would be immense positive jerk within the first fraction of a second.

After the initial acceleration, determined mostly by the tires and the maximum torque of the engine, we are mostly limited by the specs of cars engine to deliver power. When the car is moving at a constant velocity, it requires more power to accelerate and since this is limited, the acceleration will drop (my Toyota Corolla can pull me back to my seat, but I cannot overtake a truck since accelerating from 80km/h to 100km/h takes too much time). Therefore, it seems that there is negative jerk just in accelerating the car at full throttle.

Here is a velocity of a car I found on the internet. You can see that the first derivative of position has a negative second derivative (negative curvature) indicating that the third time derivative of position is negative (negative jerk).

_{(source: slotforum.com)}

Now to your actual question: is moving the throttle position a good example of a jerk? I do not really know what is derivative of induced acceleration with respect to throttle position. In old engines it adjusts an air valve, but the air intake (power) must also be dependent on the RPM. Based on this, I would say that easiet illustration of jerk would be the initial acceleration boost (not pulled back to seat --> pulled back to seat).

Answer 4

The claim that the jerk is proportional to throttle position rests on (at least) three assumptions:

Engine power output responds instantly to throttle position. If there is any delay (think turbo lag, but other effects enter as well) it doesn't fit. Aside from turbo lag (caused by inertia of the turbine) it is probably too fast for people to notice, but some cars take a while to start accelerating even if they don't have a turbocharger.

Engine power responds linearly to throttle position. If it isn't linear, there will be fourth derivative terms.

Acceleration is linear in engine power because $a=\frac Fm-d$ where $F$ is the force of the engine, $m$ is the mass of the car, and $d$ are all the losses, assumed to be constant. This is clearly false. As the car accelerates, the air drag increases as the square of the speed. That is why when you push the accelerator down you reach a new equilibrium speed. It may be correct for a small time interval after you start accelerating when you are close to the original speed.

Answer 5

A simple way of explaining jerk to a layman is to have them imagine how their head and neck feel when riding a roller coaster.

When traveling in a straight line with no slope there is constant velocity but no acceleration. This results in no neck stress.

When in the middle of a long constant-radius turn there is a constant acceleration but no jerk. The neck muscles can easily be used to keep the head from falling to the side.

Now imagine quickly entering and exiting lots of small turns. The acceleration is changing quickly (large jerk). Even though the neck muscles might be strong enough to overcome the acceleration forces, the response time of our nervous system can't cope and the head snaps about.