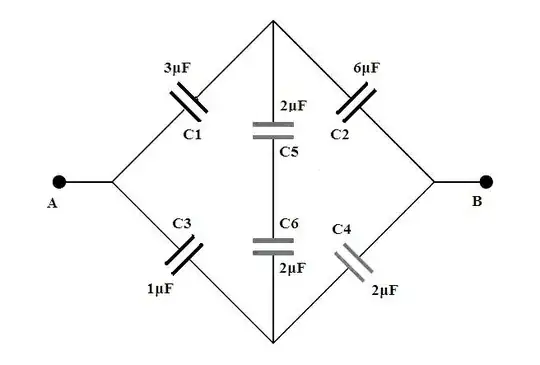
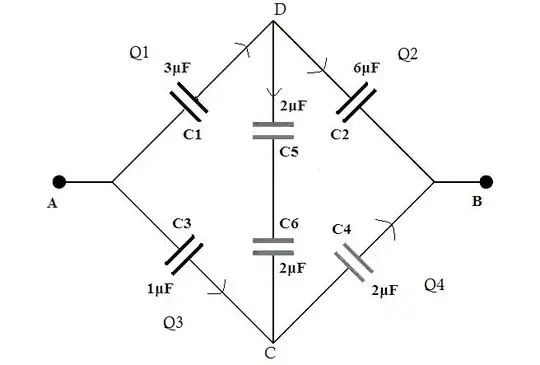
Please refer to the image below.
The question asks: 'The effective capacitance between terminals A and B in the network shown in the adjoining figure is?'
Here is my working:
(C5 and C6 connected in series.. in parallel to C2 and C4 connected in series).. connected in series with C1 and C3.
Series(C5+C6) = 1 microFarad
Series(C2+C4) = 1.5 microFarads
Parallel (1+1.5) = 2.5 microFarads
Series(C1+C3+2.5) = 15/26 microFarads (Answer)
The correct answer from the marking scheme is 8/3 microFarads. Could someone please explain how to get to this answer? I am really confused.
Thanks