If a blackbody has a temperature such that its peak frequency was well within our audible range, for example $1\ \mathrm{kHz}$, what would that sound like if we used Planck's law to plot its spectral curve in the frequency domain and performed a transformation (like an inverse FFT) to obtain a waveform?
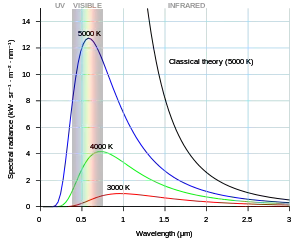
Planck's law tells us the peak wavelength and electromagnetic spectral emission curve of an ideal radiator an some temperature $T$.
If we know the peak frequency, $f$, then we can work backwards to figure its peak wavelength, $\lambda$. For our example, if $f=1\ \mathrm{kHz}$, then $\lambda\approx170\,471\ \mathrm m$, so $T\approx17\ \mathrm{nK}$.
If we plot the power spectral density of a 17 nanokelvin blackbody as a function of frequency and performed an inverse FFT on that curve, what would the resulting waveform sound like?
According to this Wikipedia article, blackbody radiation is just thermal noise (Johnson–Nyquist noise); if that's what I'm looking for, what does it sound like? Just to clarify, I'm looking for a waveform, maybe a WAV file, rather than a verbal description.