I came up with a random question which looked simple, but I can't work out the answer. The question is, why are inclined push-ups harder? And by inclined push-ups I mean push-ups with your legs on a bench or something.
I did try various ways to solve this, including moments and energy arguments, which I won't post here, but they are of no success. I made assumptions that the centre of mass of your body is half-way between your feet and your arms.
I decided to get out the bathroom scale and measure my weight at 3 different inclines; level, 16", and 30". I used a digital scale and I weighed in at 198 lbs. With 3 measurements at each hight here are the results I came up with.
Everything in lbs
30" incline 159.6 157 152.4.
16" incline 144.8 143.2 144.6
Level 137.4 139.6 144.8
Obviously they vary a decent amount likely due to my straining and slight variations in posture. Another possible factor in the accuracy is how my feet were positioned on the surface they wee on. This would include If they were hooked and some of my weight were "hanging" or the fact that the scale was always level and not in line with the incline. One more factor to consider is that the muscle you are using to lift may not be experiencing its own weight, only everything above or beyond.
I think it would be safe to say that as your feet rise, the weight you have to lift increases. Imagine slowly increasing the height of your feet to a hand stand position where you experience your full bodies weight.
Now this could be naive, but I'm inclined to think that any of the shifting around as a result of changing the angle of declination for a pushup shouldn't matter in terms of the net external force the hands have to produce. I would wager any change of measurement you find on a scale has more to do with fluids shifting in the body, and thus the center of mass changing.
For example, if one considers a very large simplification of the body as a rigid body(not a bad approximation if the athlete has good core strength) with two torques (F_g = weight, F_n = normal) acting on an axis of rotation, you can see why. Suppose there are two situations, one in which the 'rigid body' is parallel with the ground (normal pushup), and the second in which the 'rigid body' is tilted with respect to the ground:
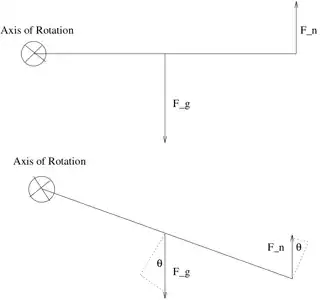
In both situations the gravitation force/weight acts through the center of mass, and the force of 'pushing' is felt via the normal force in the rigid body. In the second situation where the rod has been rotated, the torque about the axis has changed, but it changes the same for both the weight and normal vector.
This means that relatively, nothing has changed between the forces, you've made gravitational torque less 'strong' but also the normal torque less 'strong' to the same degree. Your arms will have to push with the same force as they were in the parallel case. However, this does mean there is now a compressive component to the forces, but the internal forces don't matter for a rigid body, nor would effect the torque the arms in a pushup would have to produce. The mechanics on the arms change I'm sure, and probably change the moments on the elbow and shoulder, but the overall net force required to rotate the rod/body has not changed. Therefore, I think any change in weight measure on a scale would be from a non-mechanical influence.
I'm obviously late to this. But I think the original posts calculations are probably correct. The angle of the body doesn't change the force required to rotate the body about the feet, assuming the arms are vertical in all instances.
Typically an incline push up is done against a fence or chair, in both instances the person likely holds their arms closer to perpendicular to the body rather than vertically. The angle of the arms relative to gravity makes a big difference to the maths here.
I tested this on my scales at home and if I made a concerted effort to hold my arms vertically for an incline and standard push up, I got very similar results.
So I think the change in effort required at different body angles comes more from the different muscles required ( as already highlighted here) and the inconsistencies of the angle of the arms relative to gravity.
