2

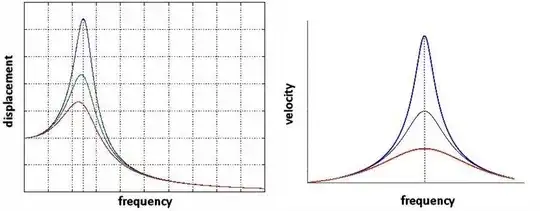
I am simulating the transient response of a mass-spring-damping system with friction. The excitation is given in the form of a base acceleration.

What I am not sure about is: can the friction change the resonance frequency of the system or will it affect only the response amplitude?

My first guess was that friction, being an external force, cannot change the resonance frequency of the system. What can happen is that there is no motion because the mass is sticked due to static friction, but if there is motion then the resonance frequency remains the same.

Then I saw that friction can be expressed as an equivalent damping as

$$c_{eq} = \mu N sign(\dot{x})$$

thus actually changing the natural frequency since it is expressed as

$$\omega = \omega_n \sqrt{1-2 \xi^2}$$

The fact is that the use of the equivalent damping is just an approximation to introduce the effect of friction into the equation of motion, is it not?

Qmechanic
  • 220,844
Rhei
  • 131

3 Answers3

2

Resonance frequency is defined as the frequency of the external force for which the external force oscillation is in phase with velocity oscillation, or, which is the same thing, for which the displacement is quarter period behind the external force. It can be shown that for damped harmonic oscillator described by the equation

$$ \ddot{x} + \gamma \dot{x} + \omega_0^2 x = f_0\cos \Omega t, $$ this frequency is

$$ \Omega = \omega_0, $$

so friction (described by $\gamma$) has no effect on the resonance frequency. It does have effect on the frequency for which the amplitude of oscillations is the largest, and the natural frequency of the damped system (which is reduced by the friction).

Ján Lalinský
  • 44,745
1

The discussion which has ensued from the question here and in A conceptual doubt regarding forced oscillations and resonance hinges on how resonance is defined for particular situations and what is meant by the natural frequency of the driven system.

An often used definition of resonance is:

Resonance is the maximum steady state response of a driven system when forced to oscillate by a constant amplitude driver system. The frequency at which this happens is the resonant frequency.

In the definition of resonance given above the interpretation of the phrase “maximum steady state response of a driven system” leads to the possibility of there being different types of resonance.

enter image description here

  • Amplitude resonance - the amplitude of the driven system is a maximum and this occurs at a frequency which depends on the amounting of damping.
  • Velocity resonance – the speed of the driven system is a maximum and this occurs at the natural frequency of the undamped driven system whether or not there is damping. This is also true of energy resonance which is characterised by maximum power (energy/time) being transferred from the driver to the driven.

In mechanical systems it is usual to talk about amplitude resonance because it is so much easier to measure a length than a speed.
However it is current (velocity) resonance which is often referred to in electrical circuit theory rather than charge (amplitude) resonance.

The resonant frequency is related to the frequency of free (natural) oscillations of the driven system.
For velocity and current resonance the resonant frequency is the natural frequency of the undamped driven system and does not depend on the amount of damping.
For amplitude resonance there is a possibility of confusion about what is meant by the natural (unforced) frequency of the system because there are two ways of defining the frequency of free oscillation of a driven system.
One is the natural frequency if there is no damping and the other is the natural frequency if there is damping.
For small amount of damping these two frequencies are approximately the same and so often the distinction between the two is often ignored.

Community
  • 1
Farcher
  • 104,498
1

The resonant frequency is equal to the natural frequency when no damping and no external force at all is applied to the system. When damping is applied so that now the decay time (decay of amplitude) is in effect, the resonant frequency decreases a little below depending on magnitude of damping.

patrick
  • 11