What is a Christoffel symbol?
I often see that Christoffel symbols describe gravitational field and at other times that they describe gravitational accelerations. Then, on some blogs and forums, people say this is wrong because Christoffel symbol is NOT a tensor and thus has no physical meaning. Which of these statements is the right one?
What is the significance of a Christoffel symbol in differential geometry and General Relaivity?
- 220,844
- 1,486
5 Answers
Here's the best way to think of the Christoffel symbols, at least for a beginner.
Suppose you want to know if/how a vector changes from one point to another in your underlying manifold, i.e. spacetime. In other words, you want to differentiate your vector field. There are two reasons that you might register a change in the vector field in your calculations:
- The vector itself might actually be different at one point than at the other OR
- The vector might be described using different basis vectors at the two points. (When you change a basis, the components of the things you're describing will change.)
Any change you detect in the vector's value from one point to another could be from either one or both of these sources.
The important point is that when assessing whether a vector (field) has changed as you go from one point to another in spacetime, you need something in your mathematics to account for the fact that your basis (i.e. your coordinate system) has changed along the way, in addition to any changes that may have occurred to the actual vector itself.
The ordinary partial derivative doesn't do this. It just assumes that the basis doesn't change. In the most general case, however, the basis vectors will change. To account for this, we replace the ordinary partial derivative with what is called the covariant derivative. The part of the covariant derivative that keeps track of changes arising from change of basis is the Christoffel symbols. They encode how much the basis vectors change as we move along the direction of the basis vectors themselves.
How is this useful in General Relativity? It's because GR models gravity as the curvature of the spacetime manifold, and information about this curvature is encoded in the Christoffel symbols.
But if the Christoffel symbols are basis-dependent (and we've just said that they are - different coordinate systems/basis vectors will give you different values for the Christoffel symbols), how can they give information about the curvature of the underlying manifold, which should be independent of coordinate system?
The Christoffel symbols don't give the curvature directly. From what we've said so far, it's clear that for the Christoffel symbols to be zero identically, the basis vectors must not change as we go from point to point. This means that we won't introduce any spurious changes to our vector fields by not accounting for change of basis.
Two things important to recognize:
Non-zero Christoffel symbols do not mean the manifold has curvature. All it means is that you are using a basis vector field that changes length and/or direction from point to point. A common example is polar coordinates on the plane. These basis vectors change from point to point, e.g. the basis vector in the theta direction gets longer the farther you get from the origin in the radial direction. This means you will have at least some non-zero Christoffel symbols. But clearly the space isn't curved.
Vanishing Christoffel symbols do not mean the space has no curvature. It might mean that you are traveling along a trajectory known as a geodesic. (This is the generalization of straight lines through ordinary flat space being 'the shortest distance between two points.') The physical counterpart of this is free-fall.
Since the Christoffel symbols let us define a covariant derivative (i.e. a derivative that takes into account how the basis vectors change), it allows us to define 'parallel transport' of a vector. I.e. the Christoffel symbol tells us what it means to say that a vector is shifted from one point to another in a way that it stays 'parallel to itself'. 'Parallel to itself' just means 'covariant derivative vanishes'.
The definition of curvature (one of them, at least) depends on this parallel transport process, which is made possible by the covariant derivative, which is in turn made possible by the Christoffel symbols.
The basic idea is that if we parallel transport a vector over a loop (i.e. coming back to our starting point), we don't necessarily end up with the same vector we started with. This is true even though we transported the vector in a 'self-parallel' manner. The crucial fact for curvature is not just that we end up with a different vector than we started with (that can happen in the case of zero curvature) but that exactly which vector we end up with depends on the path we took. So if you transport a vector 'parallel to itself' along paths a and b, you end up with two different vectors 'parallel' to the one you started with. If that happens, then by definition your space is curved.
In summary, the difference between a flat space and a curved space can be put like this: in a flat space, it's possible to build a coordinate system where the Christoffel symbols vanish everywhere, i.e. where the basis vectors are the same at every point. In a curved space, this is impossible. You can't make all the Christoffel symbols disappear in a curved space, quite simply because if you could, it just wouldn't be curved. It would be flat!
What does all this have to do with physics? Well, you can think of gravity as arising from curvature of spacetime, using rubber sheet analogies, etc. BUt I find it more helpful to think of gravity as simply arising from this need to correct for how the underlying spacetime forces us to use different basis vectors at different points. In relativity theory, the physical counterpart of 'change of basis' is change of state of motion. Just as terms arising solely from changes of basis don't reflect actual facts about vectors - only artifacts of how we choose to describe vectors - terms arising from changes in state of motion don't reflect real physical facts.
This is the heart of Einstein's extension of Galileo's revolutionary idea of relativity - that the laws of physics are what they are, regardless of your state of motion. Anything that depends on your state of motion is not a fact but an artifact and should be dismissed as such. This led Einstein (and others) to the idea that the true laws of the universe should be those that hold true regardless of coordinate system/state of motion. The Christoffel symbols can be seen as terms in the equations which make it so that they hold true for all states of motion.
So in a sense, we can say that the existence of gravity both follows from and implies that the laws of physics are the same no matter how you're moving, in the sense that if gravity didn't operate the way it does, then different observers would formulate different laws depending on their parochial perspectives (and vice versa).
- 25,615
- 723
We have the formula for the covariant derivative $$\nabla_\mu x^\nu = \partial_\mu x^\nu + \Gamma^\nu{}_{\mu\rho}x^\rho.$$ In particular, if $x^\mu$ is a coordinate vector field, then the covariant derivative is precisely the action of the Christoffel symbols on the vector field.
Now one should recognize that the covariant derivative comes from the notion of parallel transport. That is, if $x^\mu(p)$ and $x^\mu(q)$ are values of a vector field at different points $p,q$, then they cannot be directly compared. Think of a sphere - how would you compare a vector pointing west on the equator with one on the opposite side, pointing east? Well, you prescribe a procedure that takes a vector at $p$ and a curve joining $p$ and $q$ and produces a vector at $q$ -- parallel transport.
Then like the usual derivative is the infinitesimal deviation from being constant, the covariant derivative is the infinitesimal deviation from being parallely transported. Let $p(t)$ be the curve defined by starting at $p(0)$ and following a vector field $y^\nu$. Then $$x^\mu(p(0)) - Px^\mu(p(t)) = t y^\nu \nabla_\nu x^\mu + O(t^2)$$ where by the $P$ i mean that this vector should be parallel transported to $p(0)$.
(When there is a metric there is a unique notion of parallel transport and hence of covariant derivative that is compatible with the metric in the sense that all angles and lengths are preserved.)
Thus you can see that the Christoffel symbols measure the degree to which the coordinate vector fields are not parallelly transported.
Another way of understanding the Christoffel symbols is through the geodetic equation: $$\ddot{x}^\mu + \Gamma^\mu{}_{\nu\rho} \dot{x}^\nu \dot{x}^\rho = 0$$ where $\dot{x}^\mu$ is the $s$-derivative. The Christoffel symbols measure the degree to which an observer following a straight line in coordinate space is not in free fall. Such an observer, wanting Newton's second law to hold, would then have to introduce a force -- the force of gravity. This pretty much like the nature of the centrifugal force. So in a sense the Christoffel symbols and the centrifugal force are equally real and physical. (In fact, the centrifugal force can be found by starting from coordinates where the Christoffel symbols all vanish and going to a rotating system.)
However, the centrifugal force can always be made to go away. You only need to find the angular velocity as a function of time, the condition is an ODE, you can always solve ODEs. But the Christoffel symbols can depend on space. The relevant condition is then a set of PDEs, and systems of PDEs come with integrability conditions that essentially come from $\partial_x \partial_y = \partial_x \partial_y$. They are not always satisfied! For the Christoffel symbols, the integrability condition is precisely that the Riemann tensor should vanish. The Riemann tensor is, well, a tensor, so no one will claim that it isn't physical.
You can be less restrictive and only require that the Christoffel symbols vanish along a geodesic. You can do this by picking one of the coordinates to be the proper time of an observer moving along the geodesic. This is why it is sometimes said that gravitation is not a force. If you think the centrifugal force is fictitious then maybe you should think that also of gravitation. But that this is only true locally, along a single geodesic at a time, shows that there is something more real to gravitation. It's not just a bad choice of coordinates because there may exist no good coordinates. And the Riemann tensor quantifies the obstruction to that.
- 15,017
Christoffel symbols do not describe gravitational fields, nor do they describe accelerations. Rather, they are related to the Levi-Civita connections that can be used to describe geodesics onto manifold with any general metric. In this respect, being general relativity a metric theory, they will eventually show up whilst calculating the equations of motion for moving particles.
To be more precise: given a covariant derivative $\nabla$ on a Riemannian manifold one defines the connection coefficients $\Gamma$ as $$ \nabla_{\mu}e_{\nu}=\Gamma^{\lambda}_{\phantom{\lambda}\mu\nu}e_{\lambda}. $$ If the covariant derivative is compatible with the metric, i. e. if the scalar product of two vectors is left unchanged along parallel curves, then the connections coefficient can be expressed back in terms of the metric and the torsion as $$ \Gamma^{\lambda}_{\phantom{\lambda}\mu\nu} = \{\lambda \mu\nu\}+ \textrm{torsion} $$ with the Christoffel symbols $$ \{\lambda \mu\nu\} = \frac{1}{2}g^{\lambda\rho}\left(\partial_{\mu}g_{\nu\rho} + \partial_{\nu}g_{\mu\rho} - \partial_{\rho}g_{\mu\nu}\right). $$ If the manifold is torsion-free then the Levi-Civita connections correspond to the Christoffel symbols as derived from the metric and the geodesic equation acquires the form: $$ \ddot{x}^{\mu} + \Gamma^{\mu}_{\phantom{\mu}\nu\lambda}\dot{x}^{\nu}\dot{x}^{\lambda} = 0\tag{1} $$ the derivative being the flow along the curve length on the manifold. A possible physical interpretation would be that if the Levi-Civita coefficients vanished everywhere, than the geodesic equation would simply be $\ddot{x}^{\mu}=0$, namely no acceleration along the curve is present, if you move along parallel lines, otherwise a right hand side in $(1)$ will occur, playing the role of a force accelerating the particle along the path.
In very simple cases one may calculate the above for particularly simple metric and see that the equations reduce to (some sort of) relativist Newton's law, as expected.
- 6,058
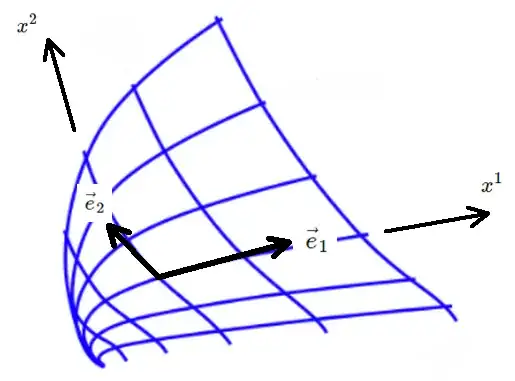
The Christoffel symbols occur as soon as you have curvilinear coordinates, even in a flat space (i.e. without any gravity or curvature).
Consider a flat space with curvilinear coordinates ($x^1, x^2, ...$).
Because of the curvilinear coordinates the tangent vectors ($\vec{e}_1, \vec{e}_2, ...$) vary from place to place. So when advancing from position $x^\beta$ to position $x^\beta+dx^\beta$ the tangent vectors change from $\vec{e}_\alpha$ to $\vec{e}_\alpha+d\vec{e}_\alpha$. You can expand these changes $d\vec{e}_\alpha$ in terms of the coordinate changes $dx^\beta$ $$d\vec{e}_\alpha=\Gamma^\mu{}_{\alpha\beta}\ \vec{e}_\mu \ dx^\beta,$$ or equivalently (using partial derivatives) $$\frac{\partial\vec{e}_\alpha}{\partial x^\beta}=\Gamma^\mu{}_{\alpha\beta}\ \vec{e}_\mu.$$
This expansion makes up a definition of the Christoffel symbols $\Gamma^\mu{}_{\alpha\beta}$ (see also at Christoffel symbols - Definition in Euclidean space). There is only geometry involved so far, no physics.
- 42,352
how i see it: The Christoffel symbols represent the correction/changes to any parallel transported vector (like particle velocity) on a curve manifold (so that this vector "stays" on a geodesic of the manifold). From Einstein equations, the energy/matter forges the structure of the (spacetime) manifold, and this structure is expressed by the metric tensor (that is solution of Einstein equations). The Christoffel symbols are directly linked to the metric tensor and so they "force" any moving particle to follow a geodesic on the manifold. In that sense the Christoffel symbols can be seen as the components of a force field (the gravitational field) that at any point of the manifold will force the particle to follow the (curved) structure of spacetime. In this context the metric tensor can be seen as the source of the (gravitational field) potential.
- 11