I went back and took a more careful look at this. I'm still not convinced it's correct, but I'm hoping this is at least better than what I had before.
Let $h$ be the height of the column of water inside the straw. As this height rises by an amount $\delta h$, the work done on the column is
$$\delta W = P A \delta h$$
where $A$ is the cross-sectional area. The change in potential energy is
$$\delta U = \rho A \delta h g h$$
so by conservation of energy,
$$\delta K = \delta W - \delta U = \left(P - \rho g h\right) A \delta h$$
This excess kinetic energy comes from two contributions: the added mass,
$$\delta K_1 = \frac{1}{2}mv^2 = \frac{1}{2}(\rho A \delta h)\dot{h}^2$$
and any change in speed of the column of water,
$$\delta K_2 = \frac{1}{2}m(2v\delta v) = (\rho A h)\dot{h} \delta\dot{h}$$
Putting it all together, we get
$$P A \delta h - \rho A g h \delta h = \frac{1}{2}\rho A \dot{h}^2 \delta h + \rho A h\dot{h}\delta\dot{h}$$
If you assume (or prove) that $P$ is dependent on $h$ through Bernoulli's theorem,
$$P + \frac{1}{2}\rho\dot{h}^2 = P_0$$
Substituting in (and canceling the common factor of $A$), you get
$$P_0 \delta h - \rho g h \delta h = \rho \dot{h}^2 \delta h + \rho h \dot{h}\delta\dot{h}$$
which at least accounts for the mysterious factor of $\frac{1}{2}$ that appeared in previous versions of my answer.
Now, I don't think we can simply assume that $\delta h \neq 0$ and divide it out, because if we do that, we get a factor of $\frac{\delta\dot{h}}{\delta h}$ which is undefined at the initial and maximum heights. (Roughly speaking, the variation $\delta h$ is second-order at those points whereas the variation $\delta\dot{h}$ is still first-order.) Instead, I'll divide by $\delta t$, which certainly should not produce any singularities, to get
$$P_0 \dot{h} - \rho g h \dot{h} = \rho \dot{h}^3 + \rho h \dot{h}\ddot{h}$$
At the initial and maximum heights, $\dot{h} = 0$, so the equation is trivially satisfied there. But consider the situation when displaced from either initial or maximum height by an arbitrarily small amount, such that $\dot{h}\neq 0$. Here we can cancel out $\dot{h}$ to get
$$P_0 - \rho g h = \rho \dot{h}^2 + \rho h \ddot{h}$$
Since $\dot{h}$ will be infinitesimally small around the maximum height, we can neglect the first term on the right, but not the second. So we're left with
$$P_0 - \rho g h = \rho h \ddot{h}$$
Note that this agrees with a simple analysis using Newton's second law. (The forces acting on the column of water at its maximum height are the pressure force $P_0 A$ acting upwards and gravity $\rho Ahg$ acting downwards, and the difference is equal to $ma = \rho Ah\ddot{h}$.) So the differential equation passes at least one basic consistency test.
Anyway, this equation no longer admits the solution $h = \frac{P_0}{\rho g}$. Instead we have
$$h = \frac{P_0}{\rho (g + \ddot{h})}$$
Unfortunately I can't think of a way to determine $\ddot{h}$ at maximum without solving the equation, so for now I'm limited to a numerical solution.
For a quick estimation, I plugged the full differential equation from above into Mathematica's NDSolve function. With boundary conditions $h(0) = 0$ and $\dot{h}(0) = 0$, it complained about undefined expressions, so I used boundary conditions at a nonzero time,
$$h(\epsilon_t) = \epsilon_h$$
and
$$\dot{h}(\epsilon_t) = \epsilon_{\dot{h}}$$
for values of the various $\epsilon$ constants ranging from $10^{-3}$ to $10^{-8}$. In my tests, I get this graph, seemingly independently of the values of $\{\epsilon\}$ or the ratios between them:
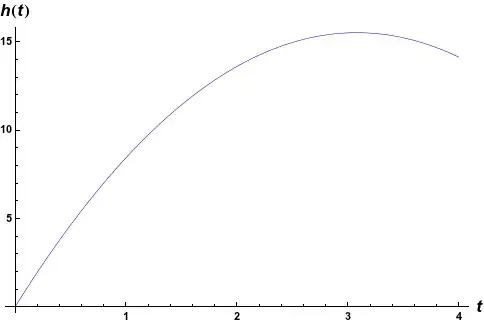
Mathematica indicates that the graph peaks at $15.5\,\mathrm{m}$, so if this analysis is correct, that would be the maximum height. (FWIW I am still very suspicious of this calculation though)

