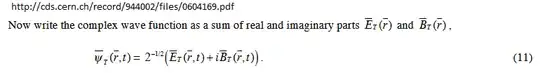How energy of a photon or EM wave has something to do with frequency?

Question

While I was thinking what exactly meant by energy in quantum mechanics, I was quite shocked by the fact that it is proportional to frequency.

$$E=hf$$

Given the fundamental definition of energy in classical mechanics is work done which is exactly energy transformed. (in newton mechanics, you get conservation of energy from this definition)

Now given Photoelectric effect, assuming light is indeed EM waves, now it seems to me indeed strange that electrons get more energy by a higher frequency. Since frequency has pretty much nothing to do with either "force" or "distance" in the fundamental definition above.

I wonder if this is how classical mechanics fails to predict Photoelectric effect? Is my reasoning correct? It seems something is missing in my reasoning, but I am not sure what it is.

Or perhaps, I should ask myself a counter question: how energy of a photon or EM wave has something to do with frequency?

---

Edited: Now I remember there is such a thing as Poynting vector. But I am still kind of confused, because Poynting vector is proportional to $\text{cos}^2(kr-wt)$, frequency's effect on energy density flux is bounded from zero to one. Perhaps I should ask another question about that.

Answer 1

The connection of frequency to energy comes when one considers the covariant formulation of the electromagnetic wave propagation. In Panofski and Philips "classical electricity and magnetism" second edition chapter 21.

This quote in particular.

This associates a zero mass particle with a fourvector, i.e. energy and momentum .

Text goes on to explain doppler shift in electromagnetic waves.

This answers your:

Or perhaps, I should ask myself a counter question: how energy of a photon or EM wave has something to do with frequency?

After all classical electrodynamics is a highly mathematical theory, which has been extremely successful in describing the behavior of charges, magnetism and radiation.

The question in the title:

How energy of a photon or EM wave has something to do with frequency

has been answered as far as the classical EM wave goes. Photons, as zero mass elementary particles have only energy/momentum, E=h*nu, and spin +,-1 in their direction of motion. The frequency is hiding in the quantum mechanical wave function of the photon

In the E and B fields that a multitude of photons will build up in a beam.

The specific formula though is an experimental measurement, coming from the black body radiation measured curves, which did not show the ultraviolet catastrophy expected from the above classical frequency to energy connection.

Planck calculated the constant which would fit observations of quantized energy increments. Together with the photoelectric effect black body radiation was one of the reasons that quantization of the microworld was necessary.

Answer 2

it seems to me indeed strange that electrons get more energy by a higher frequency

Why is it the high-frequency part that bothers you? Classically, high frequencies imply more energy. An example you might consider is whacking a ball-- the faster it spins, the higher it's frequency and the more rotational energy it has. More relevant, high frequency photons (like x-rays and gamma rays) have more energy than low frequency photons (like radio waves). It's expected that electrons would get more energy if they were "hit" with a higher energy photon

Answer 3

Both photons or particles like electrons both exhibit wave-particle duality. In classical mechanics we do not just say more frequency gives more energy because with most oscillations or waves the energy depends on amplitude too. The Plank equation $E=hf$ is not a classical idea. It is not going to be obvious at all. It took hundreds of years of hard thinking and Nobel prizes to get there. Similarly on classical lines there is no reason to say more momentum give less wavelength. As stated in the other QM equation of deBroglie $p=h/\lambda$. (Additionally the photon spin is another quantity not related to its wave frequency as was speculated in another answer)

It's good to consider a wavetrain or wavepulse moving through a given medium not varying in time....Then we find the frequency must remain constant...if we start wiggling here ....then over there the same frequency will be observed even if there is a quite complicated intervening medium, with some limitations. Analogously in a time invariant mechanical problem the total energy (KE plus PE) will remain constant in time. (this argument is related to the $t,x$ and $w,k$ and $E,p$ argument in Panofsky& Phillips mentioned in another post .) This indeed is an important connection between Newtonian and quantum mechanics, and indicates why photon energy is proportional to frequency.

While particle spin is a "locally" defined quantity, the particle frequency is not really local because it depends on the total energy which depends on the external potential (for an electron case anyways). These questions are quite awkward as quantum mechanics and wave particle duality can be abstract and not very inuitive. So photon spin doesn't define its frequency, they are quite separate quantities.