The vertically downward gravitational force exerted by the Earth of mass $M$ on a object of mass $m$ standing on the surface of the Earth is given by:
$F=G\frac{m \times M}{r^2}$ where $r$ is the radius of the Earth.
Now add a dog standing close to you, also on the surface of the Earth, then the dog would exert a (negligible) more or less horizontal force of attraction on you given by:
$F'=G\frac{m \times \tilde m}{d^2}$, where $d$ is the distance between you and the dog.
Since as $F$ and $F'$ are more or less perpendicular to each other (one vertical, one horizontal) the dog does not affect $F$ in the way you describe and:
$\tilde F=G\frac{m(M+\tilde m)}{r^2}$ is not correct. See also the force diagram below:
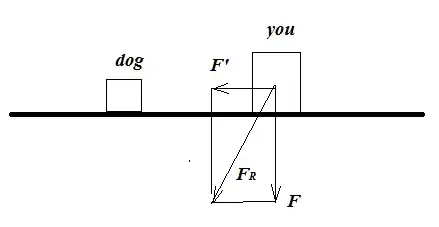
One could calculate a resultant force $F_R$ by vector addition of $F$ and $F'$. It would have the magnitude (scalar):
$F_R=\sqrt{F^2+F'^2}$ and with $F \gg F'$, then basically $F_R=F$.
