How can the unstable particles of the standard model be considered particles in their own right if they immediately decay into stable particles?

Question

How can the unstable particles of the standard model be considered particles in their own right if they immediately decay into stable particles? It would appear to a layman such as myself that these heavier unstable particles are just transient interplay of the stable forms.

Answer 1

Take for example an electron and a muon. The muon is unstable because it decays into an electron and two neutrinos in about 2$\mu$s. But a muon is not in some sense an excited electron. Both particles are excitations in a quantum field and they are both as fundamental as each other. The electron is stable only because there is no combination of lighter particles that it could decay into while conserving the total charge of $-e$ and total spin of $\tfrac{1}{2}$.

Whether a particle decays or not depends on whether there are any lighter particles for it to decay to. A muon weighs about 105.7 MeV while an electron weighs about 0.511 Mev. So a muon can transform into an electron and have 105.2 Mev left over to go into the two neutrinos and the kinetic energies of all the particles. An electron can't transform in to a muon unless it can find the extra 105.2 MeV from somewhere. If we supply the extra energy, for example in the LEP Collider, then electrons can and indeed do "decay" into muons.

Answer 2

How can the unstable particles of the standard model be considered particles in their own right if they immediately decay into stable particles?

Here I will only consider elementary, non composite particles. All the hadronic resonances are composite particles of quark antiquark combinations as well as the neutron .

The standard model of particle physics has a relatively small number of elementary point (0 dimensional) particles and is a model of a large number of observations encapsulated in their simplest form.

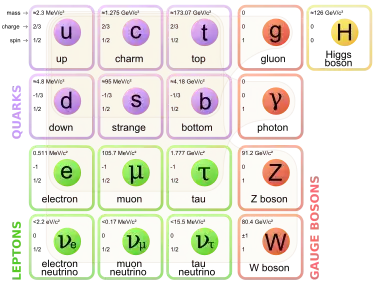
The Standard Model of elementary particles (more schematic depiction), with the three generations of matter, gauge bosons in the fourth column, and the Higgs boson in the fifth.

This model incorporates a group symmetry ( SU(3)xSU(2)xU(1) ) which identifies it. The basic hypothesis is that at large energies the symmetry is unbroken, i.e. that there exists no Higgs field to give masses to the particles entering in the table, and thus at those energies all these particles are stable, since there cannot be a lower energy state to which they can decay. They have a separate existence in the group symmetries due to the quantum numbers which give a unique niche for each particle.

After the electroweak symmetry is broken at about 246 GeV and below , the Higgs vacuum expectation value, the particles acquire the masses we have measured in the laboratory and the composites display the beautiful group representations that gave rise to the standard model to begin with.

It would appear to a layman such as myself that these heavier unstable particles are just transient interplay of the stable forms.

The standard model says that the unstable particles are an artifact of the low energy in which one observes them, at high enough energies they are no longer unstable because they have zero mass.

The standard model took years to develop. When I started in 1963, different models,( four fermi interactions, vector meson dominance, Regge poles,eightfold way) were in fashion, which due to the accumulation of data slowly morphed into the standard model. It is the different quantum numbers, conserved by different interactions, that give the particular group structures observed and finally the particle table.

It is interesting to note though, that string theories, which can embed the standard model of particle physics, posit one kind of "particle", instead of a point , a one dimensional string where the particles are vibrational levels of the string which display the standard model group representations.

Answer 3

I think the most direct answer to this would be the fact that a heavier particle can decay into many different lighter particles for different reactions. The abundance of occurence of these relations are const. Again the same heavy particle can be created in multiple types of collisions of various different lighter particles. Thus we cannot say that the heavier particle is just "composite particle".

Although there are some particles of this category you mentioned. For instance "composite fermions" which are bound state of a electron and flux quanta. But not all.

Answer 4

Inmediately is not really true, there is some proportionality.

Sorry I am not answering directly about "the standard model", this is quarks and leptons. But they will fit the general pattern, you will see. Let me first consider all the "particles" listed in the particle data group file.

Most of the particles decaying via photons have a half-live about inverse the cube of its mass, times a constant.

Most of the particles decaying via beta have a half-live about inverse the fifth power of its mass, time a constant.

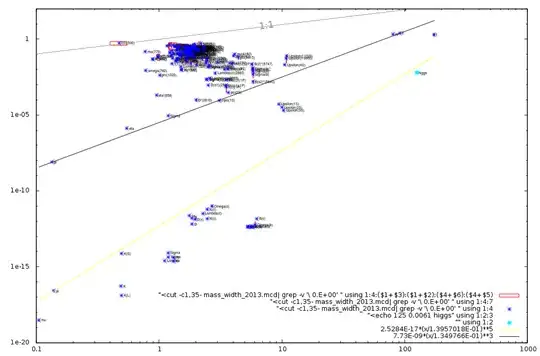
See here the picture. Horizontal is mass, vertical is decay width, which is about the inverse of halflife.

The neutron is a lot more stable, so it is not pictured here, it is down in the plot then.

The "resonances" and "excited states" are in the huge clud with very small lifetimes, or wide decay widths. So even if W, Z or the top decay faster than any resonance, they decay slow enough compared with its mass. Still, even a resonance is more stable that the inverse of its mass, $ t_{1/2} > \hbar / mc^2$, the grey line above in the drawing

Even for the Higgs (the decay width has not been really measured directly yet, same that for Upsilon 1,2 and 3, but anyway we can guess or calculate them) you can see that it is stable enough compared to its mass. Also, there is still some unmeasured excited states of Bs which should be between the two lines, and it seems it is not going to get a name, just Bs* will be. So it is something of a thumb rule, but it looks acceptable when you plot everything. Amusingly most textbooks seem not to have space for a such nice log plot.

So, at the end, what about the standard model fermions? Well, as charge is preserved, and accidentally also baryon and lepton number, they only decay via the weak force. You can see in fact the "mu" exactly in the low corner of the plot, and a imaginary $m^5$ line across it will cross the tau lepton too. Thus they are all more stable that the yellow line in the plot, except the top, which is middle between both, due to the restauration of electroweak symmetry. So for the fermions, As for W and Z, and Higgs, they also conform with the intuitive scale. Say that, they are all more "fundamental" and we would surely consider them particles in its own right even if they were not as stable as they are. But they are very stable.

Answer 5

How can the unstable particles of the standard model be considered particles in their own right if they immediately decay into stable particles?

Nobody has an issue calling the electron a particle. Ditto for a neutron. It's stable in a nucleus, and the fact that a free neutron decays in circa 15 minutes doesn't much matter. It's similar for a muon, which lasts for a couple of microseconds, because that's quite a long time in particle physics. Muons leave tracks, as do other non-stable particles. And because we can see those tracks, I don't think many people have an issue calling them particles.

Things start to get interesting when we move on to shortlived baryons where you hear the word "resonance". I'm afraid to say I always think of a twanged ruler when I hear that. Something that doesn't last, that's more of an action or an event than a thing. Particularly when it comes to the Z-boson which lasts for circa 3 x 10$^{-25}$ seconds. Nobody has actually seen a Z-boson, or a track. Its existence is inferred. It's similar for some other particles: "Experiments don’t detect the Higgs boson directly – instead, its existence is inferred by looking at the particles left behind when it decays".

It would appear to a layman such as myself that these heavier unstable particles are just transient interplay of the stable forms

I guess particle physicists call them particles, and everybody else goes along with that. But maybe somebody like anna v can give a better answer.

Answer 6

You're question is interesting because it is connected to the notion of elementary particle. As mentioned by anna v, the elementary particles (fermions) of the standard model have very specific properties under the symmetry of the standard model ($SU(2)_L\times U(1)_Y \times SU(3)_c$): they lie in the fundamental representation of the group, which in familiar language means that they are the building block of all other particles (baryons, mesons etc). This definition does not imply that elementary particles are necessarily stable. An electron, a muon and a tau (3 elementary particles, leptons) have exactly the same property under a transformation of the symmetry group. Nothing distinguishes one from the others except their mass. Heavier particles can decay into the lighter ones.

Answer 7

Your question seems quite general, but perhaps you're confused about what "decay" is. When we say something "decays" we don't always mean that it's somehow "breaking up" into it's constituent parts. In fact, we hardly ever do. The heavier particles aren't really "transient interplay of the stable forms", unless I misunderstand, and that isn't something that it makes sense to say.