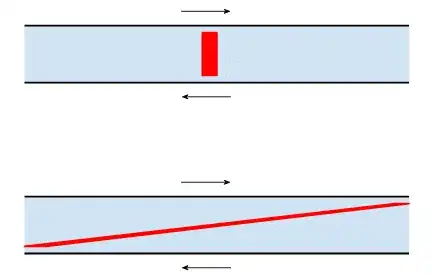
Two typical quantities which characterize these systems are the Reynolds and Schmidt number:
$$\mathrm{Re}=\frac{vL}{\nu} \qquad \mathrm{Sc}=\frac{\nu}{\mathcal{D}}$$
where $v$ and $L$ are characteristic velocity and length scales and $\nu$ and $\mathcal{D}$ are the kinematic viscosity and the diffusion coefficient (both material properties).
These characterize the system because each describes a certain regime:
- The Reynolds number is the relative importance of convective to viscous transport; for $\mathrm{Re}\ll1$ viscosity dominates, for $\mathrm{Re}\gg1$ inertia dominates.
- The Schmidt number is the relative importance of momentum diffusion to mass diffusion; for $\mathrm{Sc}\ll1$ mass diffusion dominates, for $\mathrm{Sc}\gg1$ momentum diffusion dominates.
Combined we can say something about the relative important of mass diffusion to convective and viscous transport. It is also typical to define a Peclet number (which is simply the product of the Reynolds and Schmidt number) which then describes the relative importance of convective transport to mass diffusion:
$$\mathrm{Pe}=\mathrm{Re}\mathrm{Sc}$$
Now in the video there are some keywords which can help us estimate these value; high viscosity liquid (i.e. corn syrup) and that the system is turned slowly. This indicated that we are dealing with a very low Reynolds number (i.e. $\mathrm{Re}\ll1$) system where viscosity dominates (also known as the laminar regime).
Estimating the Schmidt number requires knowing the kinematic viscosity and diffusion coefficient. The viscosity of corn syrup is known to be around $10^{-3}$ $\left[m^2/s\right]$ (about $10^3$ times greater than water). Unfortunately, knowing the diffusion coefficient of corn syrup in corn syrup is more difficult to obtain; so let's assume a typical value of $10^{-9}\left[m^2/s\right]$ for liquids. We then estimate $\mathrm{Sc}\sim
10^6$ which indicates that momentum diffusion is much more important than mass diffusion in this system. As for the Peclet number, with the calculated values this is most likely $\mathrm{Pe}\gt1$ which indicates that convective transport is at least as important as mass diffusion but as convective transport was already less important than viscous transport this doesn't give us any new information.
Concluding this analysis, we can say that the reason why the system returns to its original state is simply because we are dealing with a laminar system in which the time scales involved are not large enough for mass diffusion to be of any importance and smear out the dyes.