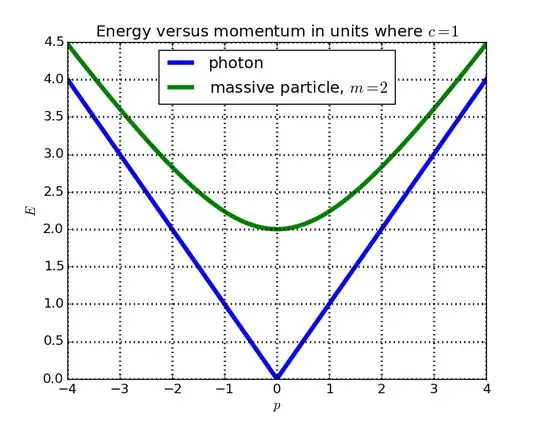
A photon has rest $m=0$, but it is never at rest, so it has no rest mass, then the relativistic mass is according to me non-zero because:
- $E = \text{work}=m \times \text{acceleration} \times \text{displacement}$, if $m=0$ then $E=0$, which it is not
- Light is trapped in a black hole
- In the de-Broglie equation, $\lambda=h / (mc)$, if $m=0$, the expression is undefined, alternatively I can find the mass of a photon applying the wavelenghth of light in lamda
- Light has momentum and energy, which is I think impossible with a zero mass.
I dont have a very vast knowledge in physics, please tell me where in each of this 4 cases I am wrong.