Regarding synchronization of clocks in special relativity

Question

I am trying to read of synchronization of two clocks in same inertial frame in special relativity. Suppose we have two synchronized clocks in an inertial frame placed at positions $x_1$ and $x_2$ in that frame. Suppose two observers at $x_1$ and and $x_2$ try to measure speed of some object moving in between $x_1$ and $x_2$(not at the midpoint or any close) with a constant speed. Now both observers, watch the object travel the distance $ \Delta x$. Let the object be closer to $x_1$. The observer at $x_1$ records times at which the object enters the $\Delta x$ region and another when it leaves the region. Lets call them $t_1$ and $t'_1$ and similarly the observer at $x_2$ records $t_2$ and $t'_2$.

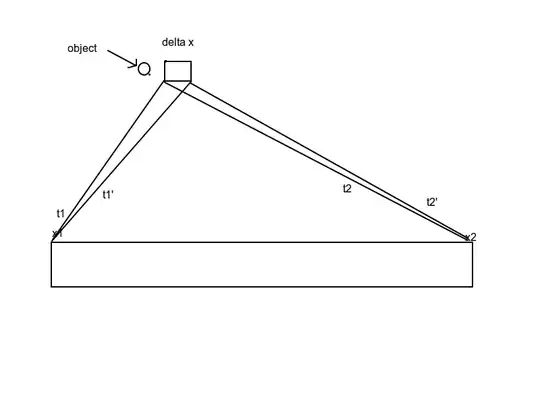
Now the time difference between $t_1$ and $t'_1$ is should not be same as the difference between $t2$ and $t'2$ since the light travels at a finite speed. So the velocities as measure by $x_1$ and $x_2$ observers should be different because the time intervals measured by them are different. This would imply both the observers measure different speeds. But I am wondering how is this possible? How can an object have two different speeds in same inertial frames? Am I missing something?

(PS: sorry for bad figure)

Answer 1

Suppose as the object enters $\Delta$x, it hits an antenna which sends a signal to $x_1$. $x_1$ proceeds to record the time. It also does the same for $x_2$, who also records the time. A similar signal is sent when it leaves $\Delta$x.

Yes the light signal will take a longer time to reach $x_2$, and thus the signals will reach $x_2$ at different times, but for someone in the same frame as $x_1$ and $x_2$ the time difference $x_1$ and $x_2$ measure will be the same.

The spec.relativity bit comes in when you look at the reference frame of the object. The events will no longer be simultaneous.

Answer 2

There is a fundamental flaw in your setup. While the actual times the entrance signals may reach clocks 1 and 2 could be different, $t_1'-t_1$ will be the same as $t_2'-t_2$, because the clocks are at rest with respect to each other.

In fact, consider there are two events: entrance and exit. SR says that $$c^2\Delta t^2 - \Delta x ^2 = c^2\Delta t'^2-\Delta x'^2$$ for all inertial reference frames observing the two events. You agree that your observers in the same reference frame as each other measure the same $\Delta x$ as each other. Then they must measure the same $\Delta t$ or the equality wouldn't hold.

Answer 3

In order to measure the velocity in your setup, you have to measure the actual time difference for the object entering and exiting the region $\Delta x$, not the time difference seen by a distant observer receiving signals of the entrance and exit. There are (at least) two ways to do this.

For example, station toll-takers at the locations where the object will enter and exit the region $\Delta x$, call them $x_i$ and $x_f$. These are in the same reference frame as $x_1$ and $x_2$. Give them clocks and get all four clocks synchronized. Then $x_i$ will record the time $t_i$ when the object passes through his toll gate and enters $\Delta x$, and $x_f$ will record the time $t_f$ when the object passes through her toll gate and exits $\Delta x$. Afterwards everyone shares the two times, and since we know the distance $x_f - x_i = \Delta x$ we can calculate velocity. This is the velocity in the reference frame of $x_1$ and $x_2$.

To do the calculation the way you want to do it, the observers $x_1$ and $x_2$ need to know how far they are from the points I called $x_i$ and $x_f$, and they need to use that information to figure out the delay between when the object passed $x_i$ and when they actually observed it at their distant locations or received the signal that the event had occurred. Although $t_1 \ne t_2$, if the distances and the speed of the signal propagation are known, both observers at $x_1$ and $x_2$ will compute the same time $t_i$ and similarly the same time $t_f$. So while it is true that $t^\prime_1 - t_1 \ne t^\prime_2 - t_2$ except in a few special geometries, both observers can and must compute the same $t_f - t_i$ before they can compute the correct velocity.

Answer 4

There are 6 times in this inertial frame. Observers won't use t1/t1' or t2/t2' to calculate the true speed, rather, they need use them to calculate the orginal $t_{enter}$ and $t_{exit}$ , which will be the same for both observers.