Fourier transformation in nature/natural physics?

Question

I just came from a class on Fourier Transformations as applied to signal processing and sound. It all seems pretty abstract to me, so I was wondering if there were any physical systems that would behave like a Fourier transformation.

That is, if given a wave, a purely physical process that would "return" the Fourier transform in some meaningful way. Like, you gave it a sound wave and you would see, "Oh, there are a lot of components of frequency 1kHz...a few of frequency 10kHz...some of 500Hz..."

I've seen things happening where, if you put sand on a speaker, the sand would start to form patterns on the speakers that are related to the dominant wavelengths/fundamental frequencies of the sound. Is this some sort of natural, physical fourier transform?

Answer 1

Your ear is an effective Fourier transformer.

An ear contains many small hair cells. The hair cells differ in length, tension, and thickness, and therefore respond to different frequencies. Different hair cells are mechanically linked to ion channels in different neurons, so different neurons in the brain get activated depending on the Fourier transform of the sound you're hearing.

A piano is a Fourier analyzer for a similar reason.

A prism or diffraction grating would be a Fourier analyzer for light. It spreads out light of different frequencies, allowing us to analyze how much of each frequency is present in a given source.

Answer 2

I see that two examples in optics have been mentioned, a diffraction grating by Mark Eichenlaub, and a lens by sigoldberg1. I would like to elaborate a bit, because there is a subtle difference between the two.

On the one hand, a diffraction grating separates out light of different frequencies, i.e. colors, transforming them into different positions. This is analogous to how the 1-D Fourier transform works on a sound or electrical signal.

On the other hand, a lens takes the 2-D Fourier transform of a monochromatic light beam. Monochromatic means there is only one frequency or color. You might wonder why the Fourier transform isn't a single peak, if there's only one frequency in the light. That's because a lens transforms spatial frequencies (roughly equivalent to angles, but I will explain them below) into positions. Mathematically, this is the same Fourier transform, but it transforms an entirely different property of the light.

It took me the longest time to understand exactly what spatial frequencies were. I finally got it one day, reading chapter 4, "Fourier Optics", of Saleh and Teich's Fundamentals of Photonics, which I whole-heartedly recommend if you don't understand my explanation here.

You probably learned in your class that you can write any signal as a Fourier series, which is the sum of frequency components, each with their own amplitude and phase. The Fourier transform is a sort of continuous version of that. Well, you can express any monochromatic light beam as the sum of many plane waves traveling at different angles, all with the same frequency, but each with their own amplitude and phase. Is this starting to sound familiar? Each of these plane waves is a spatial frequency. Just as with the step from Fourier series to Fourier transform, you can make the step from discrete spatial frequencies to 2-D Fourier transform.

A positive lens focuses each of these spatial frequencies to a separate point. For example, here are illustrations of two different plane waves being focused by a lens.

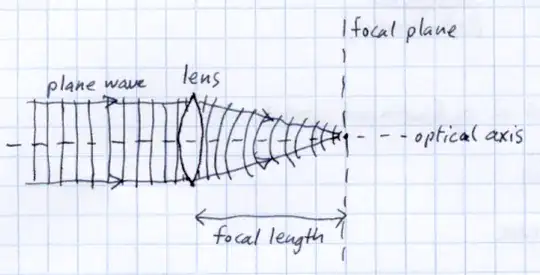
When a plane wave hits a lens face on, the lens focuses it to a point on the optical axis, at the focal distance of the lens.

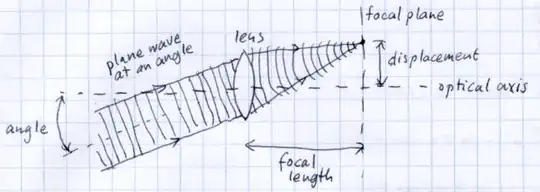
However, when the plane wave is incident at an angle, the focus is still at the focal distance, but displaced from the optical axis. This is how a lens transforms "angle" to position.

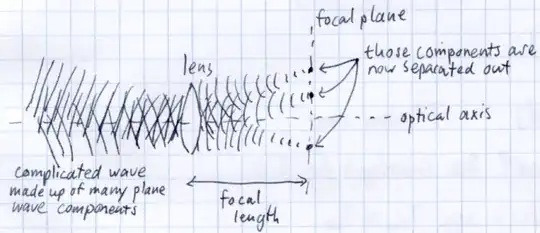
So if you have a more complicated beam made up of many spatial frequencies (which, as I said, are just plane waves), they are all focused to separate points in the same plane on the other side of the lens, one focal distance away. This is why we say it computes the 2-D Fourier transform of a monochromatic light beam. In fact, in the 1970s, when computers weren't so fast, people actually experimented with using lenses to calculate Fourier transforms instantaneously!

Answer 3

Remember the double slit experiment? The interference pattern is the Fourier transform of the hole(s). This boggled my mind when I first learned it. In the limit where the screen is far from the mask, the rays of light actually physically compute the Fourier transform (see Fraunhofer diffraction).

Answer 4

This relates to one of the coolest examples ever - lenses and how you see.

Very, very, roughly, when light interacts with a macroscopic object the result is the Fourier transform of the shape of the object, contained in the scattered light. A lens basically computes the Fourier transform of some of the scattered light. The Fourier transform is its own inverse, i.e. applied twice we get the identity. So using the lens in your eye, your retina sees the shape of the object! Same for cameras, obviously. I'll try to find some references and edit later to include them.

Answer 5

In imaging microscopy the 2D-Fourier Transform is a useful tool to analyse the images and improve the S/N ratio.

I had your same opinion at the beginning but then my boss, who actually is a FTT entusiast, was able to convince me to the actual usefulness (comic) of the technique!

Answer 6

Expounding on the 1st part of @Einchenlaub's answer (and describing my favourite example),

The Cochlea in the ear (in which the hair follicles/vibration sensors are present) is a beautiful example of how the fourier transform is carried out physically.
The changing diameter of the cochlea's tube causes different frequencies to resonate in different parts of the cochlea, so hair follicles in those regions are thus most sensitive to a particular frequency. The signals coming out of all the hair cells are the fourier transform of the incoming sound (if you organize the signals by position in the cochlea).

I believe there is research from ~2000's suggesting that human's abilities to pick out voices in a crowd utilizes this frequency discrimination; applying frequency filtering by turning "on"/"off" amplifying cells in different locations of the cochlea, effectively amplifying selected audio frequencies. (Sorry I don't have the author names etc. handy.)

Answer 7

I want to add something to the speaker issue and show that the Fourier transformation is not enough to explain it (as maybe stated implicitly by the answers provided so far).

In a first approximation you can describe the eigenfunctions of a plate subject to some mechanical (e.g. acoustic excitation) by the Helmholtz equation

$\Delta\psi(x,y) + \mathbf{k}^2\psi(x,y) = 0$ for ${x,y}\in \Omega = {(x,y)\in(-L_x...L_x,-L_y...L_y)}$

Solutions to this equation are plane waves if, and now comes the point that was not discussed so far, you have some rectangular boundary with Dirichlet conditions, say

$\psi \equiv 0$ for $(x,y) \in \partial\Omega$

Then, you really have (the m'th) resonances/eigenfrequencies at some $k_x*L_x = m$ and analogously for $y$.

But if the boundaries are somehow different, you get other eigenfunctions like Bessel Functions for a spherical system. The situation gets totally messi if you have a shape that is not integrable like for dynamical billiards. Then you can observe chaotic eigenfunctions.

So, to sum up, it is not enough to know the Fourier transformation to explain such wave phenomena.

Sincerely

Robert

Answer 8

A perfect example is the prism. If you pass the white light to the prism then it breaks the white light into red orange yellow,etc light signals. Its like finding the indovidual frequency components in the white light.