0

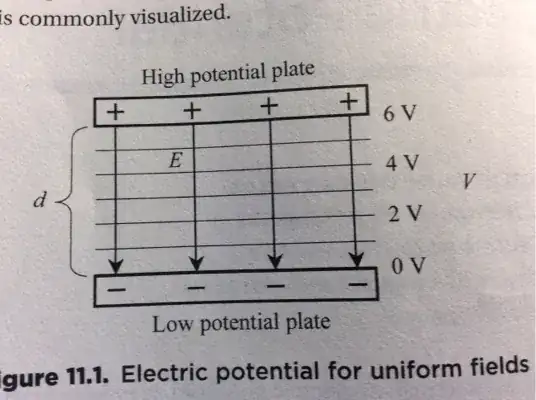
The equation: $U_E = Vq$ or $(Eq)d$.

This works the same way as the equation for gravitational potential energy: $mgh$

But to me, for charges of different signs, the potential energy also varies.

Because $d$ is measured from lowest point, usually negative plate, in the case of parallel plate for example, the direction that a particle moves in affect the distance it travel, and thus the potential energy it has.

clarification For example, a negatively charge particle, starting from 2v, would move upward towards the positive plate, which is higher potential. A positive particle would move downward. Since potential kinda is distance. The two particles would have different potential energy. But this is not shown in the equation.

See here, if the charged particle is placed at exactly the middle, sign will affect direction and thus affect the potential energy. enter image description here

Same for point charge: 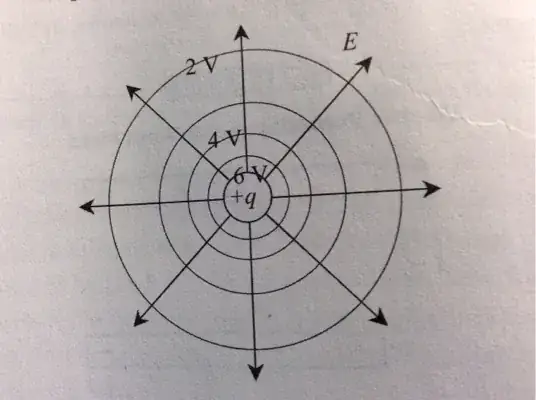enter image description here

Consider $E = k\frac{q}{r^2}$. Because "r" is the distance between the center of the particle to where the test point is located and because in this case the particle is positive, the equation would really apply if the test point placed near this particle is also positive, meaning if released, the test point would go away from it. Then the distance is not "r".

`

most venerable sir
  • 1,381

1 Answers1

2

A particle subjected to only a conservative force field, without other restrictions, will move in a direction which reduces the potential energy of the system. The particle itself does not have potential energy; the particle-field system has potential energy (some may say the field-field system, but let's not nit-pick that yet).

So what's important is not the value of the potential energy of the system, but how the potential energy changes. Based on your formula we can write $$\Delta U_E = q\Delta V.$$ That means that a negative charge will move toward higher $V$ under the influence of the external $E$ field. A positive charge will move toward a lower $V$. The actual values of $V_{initial}$ and $V_{final}$ are irrelevant as long as $$V_{final}-V_{initial}=\Delta V$$ arithmetically has the correct sign.

An electron and a proton placed in the same field (separately, so they don't influence each other) will move in opposite directions. They are opposite sign and their unrestricted movements must reduce the system potential energy.

Bill N
  • 15,522