Ewald summation without repeating one particle periodically?

Question

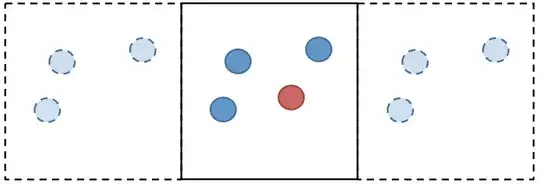
I need to perform an Ewald summation for a Brownian Dynamics simulation. In the normal Ewald summation procedure, all particles in the simulation box are periodically repeated in the neighbouring boxes. Is it possible to alter the Ewald summation in such a way, that one particle is not periodically repeated? (I included a sketch for clarity. The red particle is not repeated in the neighbouring boxes.)

In my case, I look at many static particles that interact hydrodynamically (Rotne-Prager Tensor) with one dynamic tracer particle. So, in a sense, I would like to sum the hydrodynamic interactions between the tracer and all periodic images of the static particles.

Answer 1

I found the answer to my question myself. Simply put, the answer is 'no'. The reason lies in the definition of the lattice sum (equation 2 in Beenakkers original paper 'Ewald sum of the Rotne-Prager Tensor' from 1986). Due to the symmetry of the system, it can be reduced to a 3Nx3N matrix that includes the hydrodynamic interactions of the entire system, where N is the number of particles in one periodic cell.

This definition of the lattice sum is only valid, if all particles in the system are periodically repeated.