Why we care about $d\sigma/dp^{\gamma}_{T}$? What the physical meaning of it? Why not plot $\sigma$ follow $p^{\gamma}_{T}$?. As in this picture.
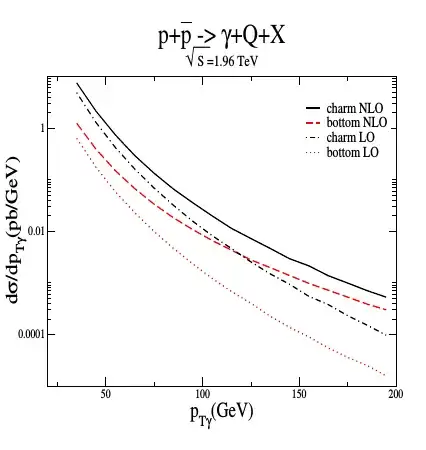
Why we care about $d\sigma/dp^{\gamma}_{T}$? What the physical meaning of it? Why not plot $\sigma$ follow $p^{\gamma}_{T}$?. As in this picture.

The differential cross section: $$ \frac{\text{d}\sigma(p\bar p \to \gamma\cdots)}{\text{d} p_T^\gamma} $$ is proportional to a probability density function (pdf) for the transverse momentum of the photon $p_T^\gamma$. In fact, if a photon is produced in the above process, the pdf for its transverse momentum would be $$ p(p_T^\gamma) = \frac{1}{\sigma}\frac{\text{d}\sigma(p\bar p \to \gamma\cdots)}{\text{d} p_T^\gamma} $$ This tells us how much $P_T$ the photon is likely to have.
This might be useful if, for example, we want to discriminate a signal from a background with the $p_T$ variable, or compare predictions with observations for the distribution of the photon's $p_T$. Note that $\sigma$ isn't a function of $p_T$ (or of the momentum of any of the final state products) because we integrate over the phase space to find the cross section, $$ \sigma = \frac{1}{2I} \int |M|^2 \text{d}^n\Phi. $$ where $\text{d}^n\Phi$ is the $n$-body phase-space of the $n$ particles produced.