Huygens' principle and why can't we see atoms with light

Question

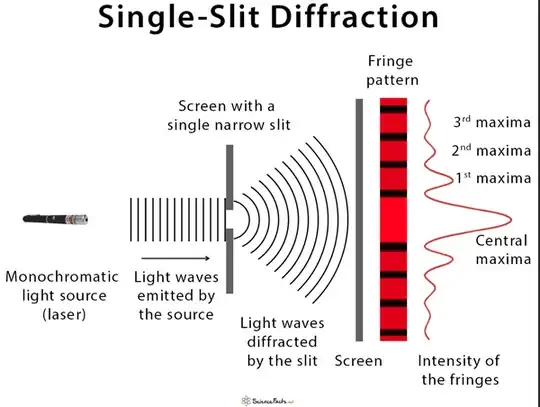
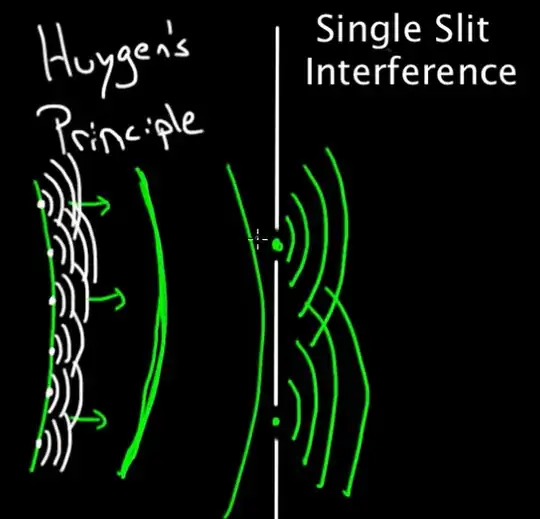
First of all, I'd like to discuss Huygen's principle. In order to explain waves diffraction, it says that every point in a wave front behaves as a source, so the next wave front is the sum of all secondary waves produced by these points. Therefore, when you make a straight wave pass through a little aperture, it spreads out. But the problem is that this spreading or diffraction depends on the size of the aperture compared to the wavelenght. Although I'm sure you've seen this many times, I'll put a video:

https://www.youtube.com/watch?v=BH0NfVUTWG4

Here you can see that when the aperture is large enough, there is almost no diffraction. But doesn't this contradicts Huygens' principle? I mean, it should spread out anyway. If every point in the aperture is a wave source, the oscilation should reach any point beyond the aperture. It is as though diffraction only happened in small holes, not in large ones nor in corners. Where am I wrong? I've read explanations for this effect with light, but they use Quantum Electrodynamics, and water waves are not quantum, right?

The second doubt I have is about seeing with light. How does light hitting a surface reflects its shape, so that it cannot reflect the shape of sufficiently small objects, such as atoms?

Answer 1

First off I think I should sort out a misconception about Huygens Principle. You can apply this principle efficiently if you have a slit, which is equal or smaller than the wavelength you are considering. If on the other hand the slit is substantially larger than the wave length, you should consider multiple Huygens sources.

Take a look at this animation

from wikipedia.

Diffraction of a plane wave when the slit width equals the wavelength

As you can read in the description of the animation, the wavelength of the waves are equal to the width of the slit and you see a nice demonstration of Huygens Principle.

However as the slit gets wider and wider the Huygens Principle breaks down and you have to consider multiple Huygens sources as it is illustrated in this diagram from wikipedia:

You can immediately see that when you make the slit larger, the diffraction effect becomes less pronounced.

Your second question is explained in this answer, I suggest you should take a look at it.

Answer 2

Unfortunately, I think you are speaking about what people commonly say is "Huygen's Principle", "In order to explain waves diffraction, it says that every point in a wave front behaves as a source, so the next wave front is the sum of all secondary waves produced by these points.", but this is not actually what Huygen's principle says.

Huygen's principle has to do with the propagation of light, which is electromagnetic waves, governed by Maxwell's equations. It can be shown that upon decoupling Maxwell's equations, one obtains spacetime wave equations of the form:

$u_{,t,t} = c^2 \left(u_{x,x} + u_{y,y} + u_{z,z}\right)$, (commas indicate partial derivatives) subject to the boundary conditions: $u(\mathbf{x},0) = u(\mathbf{x}), \quad u_{,t}(\mathbf{x},0) = \psi(\mathbf{x})$.

The solution is given by D'Alembert's formula, but in the context of space-time wave equations, is known as Kirchhoff's formula or the Poisson formula, but it is the generalization of the Huygen-Fresnel equation, and is given by:

$$u(\mathbf{x},t_{0}) = \frac{1}{4\pi c^2 t_{0}} \iint_{S} \psi(\mathbf{x})dS + \left[\frac{1}{4 \pi c^2 t_{0}} \iint_{S} \phi(\mathbf{x}) dS\right]_{,t_{0}}.$$

You see from the solution that the point of Huygen's principle is to ensure causality of wave propagation. That is, as can be seen from the solution that $u(\mathbf{x}_{0},t_{0})$ depends on the boundary conditions on the spherical surface $S = \{ |\mathbf{x}-\mathbf{x}_{0}| = c t_{0} \}$, but not on the values inside the sphere! That is, the boundary conditions influence the solution only on the spherical surface $S$ of the light cone that is produced from this point.

This is precisely Huygen's principle: Any solution of the spacetime wave equation travels at exactly the speed of light $c$. So, as you can see Huygen's principle is independent of any specific slit/aperture configuration, it will apply in any situation where you can set up such boundary conditions for the spacetime wave equation!

Answer 3

I would be able to answer your first doubt , which is that if an aperture is large enough , it violates the Huygens's principle .

My view : In the one-slit experiment , If I have a aperture of an appropriate size which is less than the wavelength of light , the wave undergoes diffraction , where only part of my the wave is allowed to pass the other is blocked . The part which does go through the slit where each point produces secondary waves constructively and de-constructively interfere with multiple sources leading to this observation .

But if i have an aperture larger than the wavelength of light , then in that case , I wouldn't see any diffraction becuase there is no obstacle , the obstacle is large enough to fit in the the light wave. But that doesn't mean that Huygens's principle isn't there , its just that if take multiple points on the wavefront and add them as source of secondary waves , they will lead to the same wavefront that doesn't mean , it breaks down or violates it , it simply doesn't diffract . And this is true for any kind of wave whether it be light or water , both follow the same thing .

I hope it helps !