How can laser interferometry be used to measure path difference smaller than wavelength of laser light?

Question

The currently proposed Gravitational wave detection apparatus consists of Michelson Interferometer which is supposed to measure distances of the order of $10^{-22}$m. But the wavelength of the light used is in the order of micrometers ($10^{-6}$m). How is this possible? The conventional way to measure distance is by counting the interference fringes. But for path difference smaller than wavelength of laser light this is not possible.

Answer 1

The measure is done by looking at the intensity of the light exiting from the interferometer.

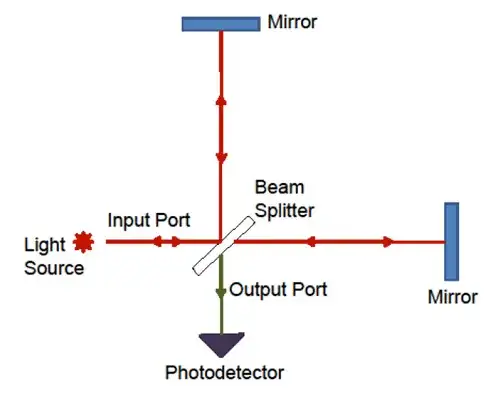
Looking at the scheme in figure you can suppose for simplicity that the light source inject a plane electromagnetic wave in the input port. The light is splitted in two parts by the beam splitter, and then recombined. If the field at the input port is given by the real part of

$$E_{in} = E_0 \exp\left( -i \omega t \right)$$

the contribution that arrives at the output port after traveling in the vertical arm of the interferometer will be

$$E_{1} = r t E_0 \exp\left( 2 ik L_1 -i \omega t \right)$$

where $L_1$ is the length of the vertical arm and $r$, $t$ the reflection and transmission coefficient of the mirror. Similarly the contribution from the field traveling in the horizontal arm will be

$$E_{2} = -r t E_0 \exp\left( 2 ik L_2 -i \omega t \right)$$

The square amplitude of the output field will be given by

$$\frac{1}{2} \left|E_{1}+E_{2}\right|^2 = r^2 t^2 \left[1-\cos \left(4\pi \frac{L_1-L_2}{\lambda}\right) \right] $$

The point here is that this intensity, which can be measured using a photodector, is a function of the difference $L_1-L_2$. The limit of the sensitivity will be given by the noises of the detector. Two important noises in the gravitational wave detectors are the shot noise of the laser, which is originated by the quantum nature of light, and the thermal noise which makes the mirror's surface to fluctuate.

Answer 2

It is astonishing that an interferometer should be able to measure distances down to 10^-12 of a wavelength.

I don’t have a detailed answer but a couple of lines of argument show how it is possible.

Reading this: http://relativity.livingreviews.org/Articles/lrr-2010-1/download/lrr-2010-1Color.pdf (also linked by Michael Seifert above). See the amplitude of the Fabry-Perot interferometer at figure 33. The maxima are at intervals of one wavelength (lambda) but are very sharply peaked, allowing a servo mechanism tuning the apparatus to a peak to be accurate to a small fraction of lambda.

But what about Heisenberg’s uncertainty principle? Remember the thought experiment in which we measure the position of an electron with a gamma ray.

https://en.wikipedia.org/wiki/Uncertainty_principle#Heisenberg.27s_microscope

If we can measure position to much better than lambda the UP is violated! I think the answer is that this thought experiment shows the accuracy of measurement by one photon. If you measure simultaneously with many photons you can do much better. LIGO has a laser power of 100 kW in each arm, using photons of wavelength ~10^-6 m. I make that (order of magnitude) 10^37 photons per second! If you are measuring at 100Hz you have 10^35 photons per measurement.

If each photon made an independent measurement, you would expect “root N” statistics, i.e. you could improve on the variance of a single photon measurement by sqrt(10^35) ~ 10^17, which makes the reported accuracy comprehensible.

That however is a very rough argument. I doubt the measurements are independent. I think they must amount to a single quantum-mechanical measurement, that we would need to use Bose-Einstein statistics to understand. I would very much like to see a full QM calculation showing what the theoretical limit of measurement is using a set-up of this kind.

The full paper is available at Physical Review Letters and is well worth a read.

journals.aps.org/prl/pdf/10.1103/PhysRevLett.116.061102

They estimate that black holes of 36 and 29 solar masses coalesced, making a 62 solar mass black hole, and 3 solar masses * c^2 radiated away as gravitational waves, in about 1/10 second!