How can we see objects that are so far away?

Question

The HUDF used to be the deepest image of the universe ever taken by the Hubble telescope, the furthest star in this image is 59000 light years away.

The star in question:

Now Imagine a light emitting object like a star and an observer like a telescope, 59000 light years apart. I represented everything in 2D, but in 3D I suppose it would be the same but with spheres:

Now picture the photons that the object is emitting, in particle form. They will all have one direction and they will go towards this direction at C, given that there are no massive objects in between their paths:

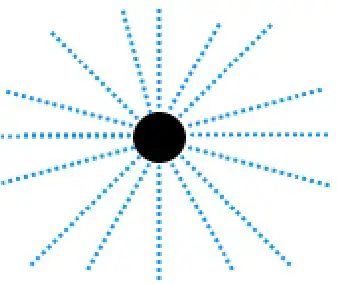
Notice how the photons have separate paths, because they have different directions, now obviously there should be a lot more photons but for simplicity I drew it like that. My point is, given enough distance shouldn't the probability of hitting a photon be so small that seeing an object becomes nearly impossible? Like so:

Here the observer can detect the photons, but if it was slightly off it wouldn't:

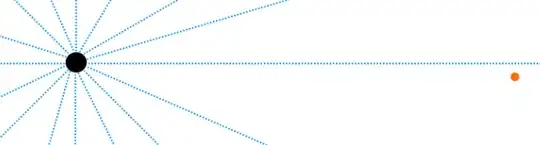
So how can we detect objects so far away? Is there something about light's wave form that I'm not considering, is this how light is emitted at all?

Update:

Looking at other duplicates questions I've seen two answers:

1- There are just too many photons being emitted that the "gaps" are just too small to make any difference.

2- This isn't really how photons are emitted, instead a quantum field is spread out radially and we only detect the photon when we interact with the field.

Does this mean that there are objects that we can't see, even if given enough time for the light to reach us (presumably outside of the current observable universe)?

Or do the gaps not exist at all because of answer number 2?

Answer 1

There are photons traveling in all directions, not just the dozen or so you show. The further from the source the telescope is, the smaller the amount of solid angle it covers and the fewer photons it will gather. A $1 m^2$ telescope pointed at the sun will receive about $1.4 kW$. Taking a typical photon energy of $2 eV$ that is about $4.2E21$ photons/second. Move the sun to $1,000,000$ light years and it is $6.3E10$ times farther, so we will get a factor $(6.3E10)^2$ less photons, but that is still about one per second.