Sorry if this question gets a little long; I want to explain why I'm asking it.
The usual Schwarzchild metric
$$ds^2 = -\left(1-\frac{2M}{r}\right) dt^2 + \left(1-\frac{2M}{r}\right)^{-1} dr^2 + r^2(d\theta^2+\sin^2\theta\ d\phi^2)$$
makes sense when $t,r$ lie in the ranges $-\infty<t<\infty$, $0<r<\infty$. We can change to Kruskal–Szekeres coordinates $u,v$ (which Wikipedia calls $X$ and $T$), which are nonsingular at the horizon. The corresponding range for them is $u+v>0$. But if we draw spacetime on the $u,v$ plane, we can see that there is no problem extending it to all possible values of the coordinates. This adds a symmetric half to spacetime, with a past singularity that behaves like a white hole: any object or light ray will eventually exit the horizon.
When I learned this in General Relativity class, the professor said that the usual physical reasoning for doing this is that the good old Schwarzschild metric is geodesically incomplete: if we imagine a particle falling into the black hole and try to trace back its path into the past, it looks like (as long as it doesn't have too much energy) it should have come up from the black hole, stopped, and then proceeded to fall in. I wasn't too convinced of this for two reasons: One, the black hole hasn't existed for all eternity so whatever is falling into it can have its origin somewhere else. Two, we haven't actually observed any white holes.
This remained a mathematical curiosity until we analyzed a Penrose diagram of the Reissner-Nordstrom metric for a charged black hole. This spacetime has two horizons and a singularity inside. But now there are timelike curves that end at some point in the future without hitting a singularity. To me this seems like a much bigger deal, since I can perfectly well imagine something falling into a charged black hole as a physically realistic situation.
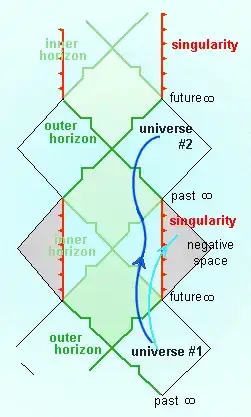
The extension in this case is something much weirder: an infinte chain of universes. You can enter a black hole here and come out at some other universe, and proceed to do the same until you get tired and settle down on some planet on whatever universe you happen to be on. This is as far from physically realistic as it gets, and yet it seems unavoidable if we want to have a charged black hole (I think the same thing happens for a rotating black hole too).
Let me state my question, then: is the incompleteness of timelike curves in a charged black hole a real thing? Is it a problem? Is the infinite tower of universes the only way to make the problem go away, and if so, wouldn't that imply that it exists in the universe, since charged and rotating black holes do exist?