There are several ways to write centripetal acceleration
$$\frac{v^2}{r} = \omega^2 r = v \omega$$
Are there intuitive explanations for any of these three forms?
For instance, I can sort of explain the form $v \omega$ by considering it as the change in the tangential velocity vector $\frac{d\theta}{dt} = \omega$ times the magnitude of the velocity vector, $v$.
What about for the other forms?
Here is one simple way.
A point is moving around a circle. It has a blue position vector and a red velocity vector, like this:
The position vector stays the same length and rotates around and around in a circle. Because the position vector is changing, it has a derivative. That derivative is the velocity.
Because we're always going the same speed, the velocity vector also stays the same length. Because the velocity is always 90 degrees rotated from the position, the velocity is also going around in a circle. In other words, the velocity vector is doing exactly the same thing as the position vector is doing; rotating and staying constant length. The only difference between the position and velocity is that we rotated by 90 degrees and multiplied the length by $v/r$.
(Note: it does not matter where we draw a vector; no matter where we draw it, the vector is the same. We draw the velocity vector at the end of the position vector, so it looks like the velocity vector is moving around in space. That's not the point. We can re-draw the velocity vector so it also starts at the origin and then it will not move around at all. What matters is just the magnitude and the direction. The velocity vector, even if we make it always start at the origin, spins around in a circle at the same speed the position vector does because they are always 90 degrees apart. So the velocity vector really looks just like a new position vector, just with a different magnitude and a direction 90 degrees ahead.)
Acceleration is the derivative of velocity, and we know how to take the derivative. Since the velocity is doing exactly the same thing the position is, we can take the derivative of the velocity in exactly the same way we did with the position.
We rotate the velocity by 90 degrees and get a vector pointed back in towards the center of the circle. That's the direction of the acceleration. Next we multiply the length of the velocity vector by $v/r$, just as before, to get the acceleration, which is $v * v/r = v^2/r$.
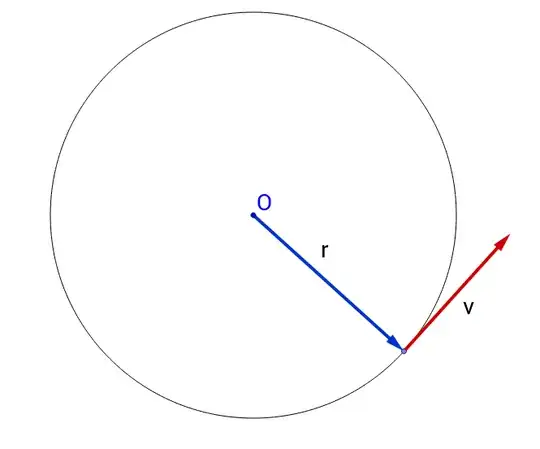
Imagine you are going in a circle of radius $r$ starting at three o'clock and heading towards two o'clock. If it takes you time $T$ then your speed is $v=2\pi r/T.$
Now if you look at your velocity it starts out going upwards then ends up going left, then down, then up again. Its like your velocity vector is on a circle of "radius" $v$ but starting at 12 o'clock (corresponding to velocity point straight up) and it also makes a full circle in time $T$ because the velocity isn't pointing straight up again until the position is at 3 o'clock again.
So we can compute the acceleration the same way we computed speed $a=2\pi v/T.$
So we have two equations and they have a $T$ we didn't want in our final answer, so solve the first equation, $v=2\pi r/T,$ for $T$ to get $T=2\pi r/v.$ Then plug that into the second equation $a=2\pi v/T$ to get $a=2\pi v/(2\pi r/v)=v^2/r.$
The first equation, $v=2\pi r/T,$ seems very intuitive and the second equation is the exact same thing happening for the exact same reason just not something we intuitively do.
It's good to be able to apply the same techniques and physical insights to problems that are functionally equivalent but less obvious, so it's a good skill to be able to do this.
If you study vector calculus you could right the equation of the particle and take the derivative a couple of times and then find the magnitude, and there isn't anything wrong with that. But you should still be able to recognize that $a=2\pi v/T$ as the rate that velocity changes.
Thinking of velocity space as a real space mean you can think of initial conditions as specifying a point in a 6d space (3 dimensions for initial positions and three for velocity) and that dynamics then moves that point around in 6d space in particular ways.
