What is the radiation force $F$ due to a beam of photons of power $P$ undergoing perfect reflection? Is it
$$a) F = 2 P / c$$
or
$$b) F = 2 P / v_g$$ where $v_g$ is the group velocity
?
Note that $v_g$ varies spatially in waveguides and in asymmetric cavities too, even in the absence of a dielectric.
The radiation pressure varies with the phase velocity of the light, not the group velocity, although you must keep in mind that the phase velocity in matter might be different from $c$ and vary with wavelength in a dispersive medium.
This has been experimentally demonstrated and described in this paper, in which it was found that the radiation force felt on a mirror will vary in direct proportion to the index of refraction of the material in which the mirror is immersed.
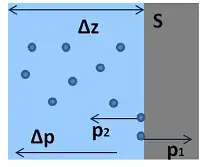
Intuitively, for higher index of refraction (slower phase velocity), there are more photons per unit length, increasing their energy density and pressure.
While the pressure on the mirror once the photons arrive will depend on the phase velocity, the group velocity still controls the rate at which information can be transferred.
Update
To be explicit, for a beam of photons with wavelength $\lambda_0$ emitted with power $P$ traveling through a medium with index of refraction $n(\lambda_0)$ impinging directly on a mirror immersed in that medium (angle of incidence is zero), the force $F$ felt by the mirror is given by
$$ F = \frac{2 n(\lambda_0) P}{c} \, \, .$$
The index of refraction is related to the phase velocity at that given wavelength, $v_{ph}(\lambda_0)$, by the relation
$$ n(\lambda_0) = \frac{c}{v_{ph}(\lambda_0)} \, \, ,$$
so that the radiation force for this single-wavelength beam can also be written as
$$ F = \frac{2 P}{v_{ph}(\lambda_0)} \, \, .$$
For light composed of a range of wavelengths, you must integrate this expression over the photon distribution of the beam with respect to wavelength, taking into account how the index of refraction varies with wavelength.
Further update (microscopic description)
Microscopically, you can think of the momentum being carried simultaneously by the E&M fields, and "an additional co-traveling momentum within the medium from the mechanical momentum of the electrons in the molecular dipoles in response to the incident traveling wave" (J.D. Jackson, Classical Electrodynamics 3rd edition, p. 262, and its corresponding reference to this paper).
See for example "Phase, Group, and Signal Velocity" about the case of a waveguide:
A waveguide imposes a "cutoff frequency" $\omega_0$ on any propagating electromagnetic waves based on the geometry of the tube, and will not sustain waves of any lower frequency. This is roughly analogous to how the pipes in a Church organ will sustain only certain resonant patterns. As a result, the dominant wave pattern of a propagating wave with a frequency of $\omega$ will have a wave number $k$ given by
$$k = \frac{1}{c} \sqrt{\omega^2-\omega_0\,^2}$$
Since (as we've seen) the phase velocity is $\omega/k$, this implies that the (dominant) phase velocity in a waveguide with cutoff frequency $\omega_0$ is
$$v_p = \frac{c}{\sqrt{{1}-\left(\frac{\omega_0}{\omega}\right)^2}}$$
Hence, not only is the phase velocity generally greater than c, it approaches infinity as $\omega$ approaches the cutoff frequency $\omega_0$. However, the speed at which information and energy actually propagates down a waveguide is the group velocity, which (as we've seen) is given by ${\mathrm d \omega}/{\mathrm d k}$. Taking the derivative of the preceding expression for $k$ with respect to $\omega$ gives
$$\frac{\mathrm d k}{\mathrm d \omega} = \frac{\omega}{c\sqrt{\omega^2-\omega_0\,^2}}$$
so the group velocity in a waveguide with cutoff frequency $\omega_0$ is
$$v_g = \frac{\mathrm d \omega}{\mathrm d k} = c {\sqrt{{1}-\left(\frac{\omega_0}{\omega}\right)^2}}$$
which of course is always less than or equal to c.
If you adopt a photonic model where the photons are seen as little particles like gas particle then the following simple demonstration indicates :
The fundamental principle of mechanics gives :
$N\frac{\triangle p}{\triangle t}=pS_{yz}$
Where N is the number of photons inside the cavity, p the radiation pressure and ${\triangle p}$ the change of momentum of every photons.
The time it takes for the photon to travel ${2\triangle z}$ is :
$\triangle t=\frac{2\triangle z}{v_{g}}$
The change of momentum of the photon is as usual:
$\triangle p=2\frac{h\nu}{c}$
though only a fraction $\frac{v_{g}}{c}$ will actually be used to act as a force against the surface S
Hence the radiation pressure gives :
$p=\frac{Nh\nu}{\mathcal{V}}(\frac{v_{g}}{c})^2$
since $\mathcal{E}_{em}=\frac{Nh\nu}{\mathcal{V}}$ we have the following expression for the radiation pressure :
$p=\mathcal{E}_{em}(\frac{v_{g}}{c})^{2}$
As in a cavity the group velocity is expressed in term of tilted plane waves $v_{g}=c.cos\theta$ then we recover the classic expression for tilted plane waves :
$p=\mathcal{E}_{em}cos^{2}\theta$
In the case of asymmetric cavity the radiation pressure has to be calculated by using the surface charges and surface currents existing on the surface of the perfect conducting walls. I do not know if a simple picture with photon can be carried out in such a case.
I would go for: $$F=\frac{2P}{c}$$ This is my reasoning: the force exerced by the light beam is due to momentum conservation. Therefore, we just have to know what the momentum of the light beam is, multiply this by 2 (because of the perfect reflection) and voilà, we have the answer.
Now, as in General Relativity, we can define the energy-momentum tensor (or stress-energy tensor depending on the crowd ^^) $T_{\mu \nu}$ (see https://en.wikipedia.org/wiki/Stress%E2%80%93energy_tensor). The first line of this matrix is the density of energy and momentum. The remaining lines gives the fluxes of those in the different directions of space. Now, it turns out that this tensor is symmetric ($T_{\mu \nu} = T_{\nu \mu}$). It means that the flux density of energy (that is the power density) in the direction $x$ for instance is the same quantity as the momentum density in the direction $x$.
The factor $c$ therefore is just a conversion factor between space and time coordinates and does not refer to the speed of the beam.
In particular, it is interesting to see that this argument is valid for any object not just light. The force exerced by a beam of massive non-relativistic (slow) particles is also $\frac{2P}{c}$. But we should be careful: the power involved takes into account every kind of energy, including mass energy. The factor $c$ that appears in $E= mc^2$ would then cancel out to give the usual expression.
