Given Inertia Tensor, Principal axes vectors, Center of Gravity, and the Moments. Is it possible to obtain object/part dimensions?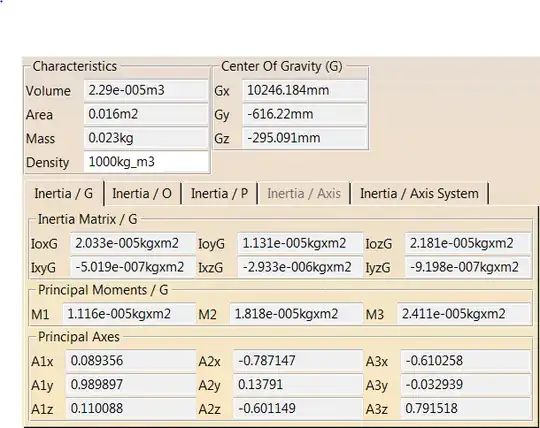
1 Answers
You can't figure out the exact shape without additional information. However, if you know basically know what the shape is, and you just need to know its spatial extent then you can figure it out from this information.
For example, supposed you know your object is supposed to be a rectangular prism. Then the only additional information you need to know about your object is the side lengths, which we will call $a$, $b$, and $c$. You can actually figure these out from the information you are given. Let's see how. In terms of $a$, $b$, and $c$, the principle moments of our prism out to be $I_1=M\dfrac{a^2+b^2}{12}$, $I_2=M\dfrac{b^2+c^2}{12}$, and $I_3=M\dfrac{c^2+a^2}{12}$. Then the radius of gyration is $R^2_g=\frac{I_1+I_2+I_3}{2M}=\dfrac{a^2+b^2+c^2}{12}$. Thus $a^2=12(R^2_g - I_1/M)$, $b^2=12(R^2_g - I_2/M)$, and $c^2=12(R^2_g - I_3/M)$. Now since you are given $I_1$, $I_2$, and $I_3$, you can find $R_g$ for your object and therefore you can find $a$, $b$, and $c$ with the above formulas.
Now suppose instead your object was an ellipsoid with principle axes $a$, $b$, and $c$. Then you could still find the lengths of the axes and the formulas would actually be the same, except there would be a 10 instead of a 12.
This shows that you can get the shape if you already know everything except the spatial extent. However if you have less information, then you can't find the shape. For example, suppose that you don't know whether you ellipsoid or a rectangular prism. You won't be able to determine which one it is from the data given. This is because you can use the above equations to find either an ellipse or a rectangular prism that would have worked. So you don't know which one it is. Of course, there are infinitely many other shapes that would have worked as well.
- 11,134