Newtonian Physics certainly precludes the existence of any 'truly' perpetual motion. Under certain conditions, we can achieve near perpetual motion by judicious application of principles and then form questions like "Although no work can be removed from the system, is the lifetime of the magnetic force in a magnet sufficient that running for several years is an acceptable answer?"
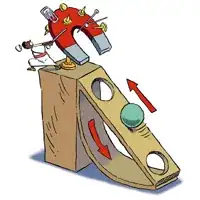
Regarding the device device shown in the question, which is a modification of John Wilkins' device similar to this one, the problems inherent in Wilkin's machine are compounded with the design shown here. Gravity is the overwhelming force to overcome in this experiment, friction plays only a small part, but we also can't overlook the current induced in the movement of the ball, which does eventually become the principle force degrading the perpetuation of motion. Here however, if the magnet was strong enough to overcome the inertia and the gravitational force of the weight on an incline, it would have sufficient energy to attach to the magnet at the top. Even without friction, and let's say that we started the ball at the top to give it an initial kinetic force, when it reached the 2nd hole, the magnet would not only have to overcome gravity, but the overall motion away from the magnet at the top, as it passed through the 2nd hole it would behave more like a skier doing a ski jump and fly away from the machine. So the magnet would also have to over come this motion, and reverse the balls direction as it is now also moving away with a velocity equal to the kinetic energy from dropping the ball minus friction.
Wilkins overcomes this with an additional ramp at the bottom, which by converting the linear motion into angular motion which reverses the direction of the ball and conserves that kinetic motion to move the ball partway up the ramp. Even so, this is not enough to overcome gravity, and friction, and the counter force of an induced current to enable it to pull the ball all the way up, while being weak enough to allow the ball to drop through the hole. I believe, but have not tested or proven, that perhaps a reduction of gravity would make this machine feasible, like on the moon. It appears also, that because the ball is made of metal that is attracted to the magnet, the forces in the ball can set up a induced current counter field, due to the material the ball is made of and its in the field. A reverse lenz effect is present that would also contribute a force the magnet would have to overcome. This would require a superfine balance between a completely attractive force, and the opposing forces. The machine looks very promising; but, on a very subtle level has counter forces from gravity, friction, and a reverse lenz effect which counter the kinetic energy built up in the balls motion which pretty much stop the action from perpetuating fairly quickly.
In the video I link, the original author of the video overcomes this effect through the pulsing of the strength of an electromagnet hidden in the base holding the permanent magnet. By turning the electromagnet off at the right moment either manually or by inductive sensing, the ball drops. So, I agree, it is very close to possible; but, it just isn't possible. I have a sense that being able to tweak gravity might be enough to make the device function under the right gravitational force, but have a real concern that eddy currents in the metal ball would provide the eventual force that would counter any possibility of it working.
As a magnetic field problem, due to Maxwell's laws and Lenz' law, the problem is a lot more complex mathematically than it looks, we tend to overlook the ball's effect on the magnetic field as it would be moving and shifting the flux density which would induce a current which would affect the movement and flux density in opposition to the movement.