To be more specific, suppose a hydrophilic infinite plate is stuck into a semi-infinite region of water, above the water is a semi-infinite region of air, when the plate is stuck into the water vertically, the contact angle is $\alpha$, as shown in the figure below:
Needless to say, the menisci on both sides are symmetric, but what will happen when the plate is inclined for an angle $\beta$? Will the contact angle $\alpha$ remain unchanged? The meniscus on which side will be higher?
To answer the question in your comment:
Yes the contact angle remains constant. The contact angle is determined by surface energies of the three materials and microscopic surface roughness, neither of which depend on the direction of gravity so tipping the plane will not effect that.
The height of the meniscus (distance from the asymptotically flat horizontal surface to the contact point) is given by: $$z=\sqrt{\frac{2\gamma}{\rho g}(1-\cos(\alpha))}$$
derived here
Where $\alpha$ is the angle of the water at the contact point relative to horizontal
The extended domain version that properly predicts both positive and negative heights is:
$$z=2\sqrt{\frac{\gamma}{\rho g}}\sin\left(\frac{\alpha}2\right)$$
For a contact angle $\theta$ and a plane tipping angle $\phi$ off vertical the heights of the two contact points would be:
$$z_1=2\sqrt{\frac{\gamma}{\rho g}}\sin\left(\frac{\pi-2\,\theta+2\,\phi}4\right)$$ $$z_2=2\sqrt{\frac{\gamma}{\rho g}}\sin\left(\frac{\pi-2\,\theta-2\,\phi}4\right)$$
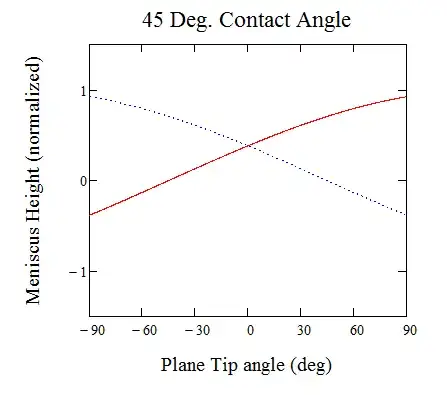
Here's a plot from horizontal to horizontal with an assumed contact angle of 45 degrees.
And here's a gif of the surface:
However, this model assumes a singular contact angle whereas real materials have contact angle hysteresis. So if we assumed ideal contact angle hysteresis, then if we start from vertical and slowly tip we'd get something more akin to this:
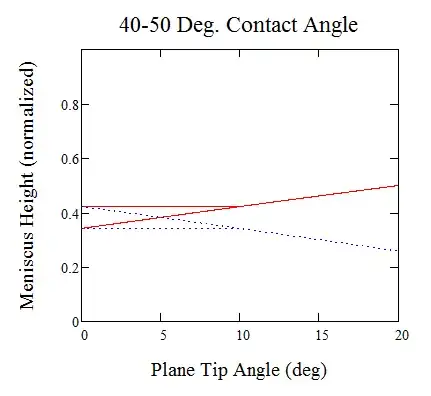
Where near the beginning there is an upper and lower bound where the height would be somewhere in-between them. This figure assumes that the rotation happens about the mean contact point. If the rotation origin were below the lower contact point then both sides would tend towards the higher limit while if the rotation origin were above both contact points then they would both tend towards the lower limits.
Section 2 of the paper below uses geometric & variational techniques to show that the Young-Dupre relation still holds for a meniscus formed by a solid of rotation that makes an arbitrary angle with the vertical:
http://www.unisanet.unisa.edu.au/staffpages/stanmiklavcic/cm_anziam2.pdf
I can't imagine that the result would be all that different if you restricted things to planar symmetry instead of the cylindrical symmetry instead. On a fundamental level, Young's relation is just a statement about the three surface tensions (solid-liquid, liquid-gas, and solid-gas), specifically that their components tangent to the surface are balanced.
the angle will change. and it will be smaller at the inclination beta. and greater at the other side
