Black Body Golf Balls

Question

The surface of a golf ball has about 35% more surface area (than a similar sphere) due to its dimples. So my question is simple, given identical radius, ideal black body material, and temperature:

Would this increased surface area allow a black body golf ball to radiate more than its smooth counterpart?

I'd like to know if the golf ball will be able to radiate its energy more quickly than the smooth sphere, so total power radiated away from the objects is what I'm interested in. By "radiated away" from the object I mean not toward it. This is energy lost by the object per unit time. There is no coolant medium, advection, convection, or conduction (to a separate object). Radiation only.

Answer 1

Consider a smooth spherical shell. The outside of the shell admits no energy transfer via radiation or any other means, so that the shell and its interior form an isolated system. The shell is at temperature $T$. Its inside surface is a perfect black body.

Next put a smooth solid sphere, also a perfect black body, in the center of the shell, also at temperature $T$. It will absorb radiation from the inside surface of the shell and will also emit radiation, all of which is absorbed by the shell. Because the shell and ball are at the same temperature, they cannot exchange net heat, so the sphere absorbs and emits radiation at the same rate.

Next replace the sphere with a perfect black body golf ball of equal cross section to the sphere. This ball absorbs the same amount of radiation from the shell as the sphere did simply because it absorbs all the radiation that hits it. The golf ball, like the solid sphere, must emit and absorb the same amount of radiation because otherwise heat would flow between bodies of equal temperature. Therefore, the golf ball emits the same amount of radiation as the sphere.

If you start with a sphere and put dimples in it, you've actually reduced the cross-section a bit because the caps of the dimples are gone, so such a dimpled sphere would radiate slightly less than before.

Answer 2

No, the golf ball would not radiate more. At http://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_law, after deriving the Stefan-Boltzmann law, it says:

Finally, this proof started out only considering a small flat surface. However, any differentiable surface can be approximated by a bunch of small flat surfaces. So long as the geometry of the surface does not cause the blackbody to reabsorb its own radiation, the total energy radiated is just the sum of the energies radiated by each surface; and the total surface area is just the sum of the areas of each surface—so this law holds for all convex blackbodies, too, so long as the surface has the same temperature throughout. The law extends to radiation from non-convex bodies by using the fact that the convex hull of a black body radiates as though it were itself a black body.

Thus, the convex hull of the golf ball is the surface that is relevant for calculating the total radiated energy. In other words, a sphere (EDIT: actually, the convex hull of the golf ball is the golf ball with the dimples replaced by discs, which has a surface area that is less than a sphere of the same radius)

Answer 3

Great question - harkens back to the days when we discussed why a tiny hole in a hot cavity is the perfect radiator and such things. Makes you think, which is what's great about it!

Would this increased surface area allow a black body golf ball to radiate more than its smooth counterpart?

The correct answer is no, it would radiate a tiny bit less than for a perfectly spherical golf ball, depending on how far away you are. If Bubba Watson is about to strike a ball on the tee directly your way, you want to be at a safe distance. How far? Let's say at least half a kilometer, i.e., 500m.

A good reference for understanding blackbody radiation and associated issues (like the "principle of detailed balance" and "Lambert's Law", which is essentially $\cos(\theta)$) is your trusty copy of Reif's "Fundamentals of Statistical and Thermal Physics".

Imagine something that's not quite a sphere - let's say two spheres connected by a long ultra-thin (massless) wire, just enough to call the arrangement a single body. Will this combination radiate more than a single sphere? Of course! But not along the line joining the two spheres, since one will be occluded by the other.

So the shape of the radiator does matter. Now let's consider the golf ball. The dimples are concave, so let's start with a single small dimple at the north pole of an otherwise smoothly spherical ball. If you are on the $z$-axis, directly above the north pole, you see the same cross-section ($\pi R^2$, where $R$ is the radius of the ball) radiating towards you. To get the exact amount of radiation you have to integrate over the surface facing you, using "Lambert's Law" alluded to above, and get the amount of radiation. The only difference from the unblemished smooth spherical golf ball case is that the dented part of the surface is slightly farther away from the observer.

To do the integral over the surface for the amount of radiation headed in a particular direction (towards the observer) you have to multiply the surface area element by $\cos(\theta)$, which is the dot product of the unit direction vector $\hat n$ and the area element $d\vec A$. This is what turns the spherical area of $2\pi R^2$ into a projected area of $\pi R^2$.

The only difference for the case of a real golf ball, and an observer viewing it from a random direction, is that the radiating surfaces are slightly farther away due to the dimples. But this is a tiny effect. If the dimples have an effective depth $d$, then for an observer at a distance $L$ large compared to the size of the ball the reduction in radiation will be the 35% dimple area estimate times $(1-d^2/L^2)$. If we estimate the effective depth to be half a millimeter, then at 500m we get roughly 1/3 of $10^{-12}$ less radiation compared to the perfectly spherical ball - a truly tiny effect.

Answer 4

Mark is correct, and my discussion with him ultimately led to an understanding, but I feel his answer lacks an intuitive approach or clear statement as to why he is correct. The simple and relevant, though not explicitly stated, portion of his answer is: emitted or absorbed radiation is dependent on the cross sectional area and not the surface area.

By using a gaussian surface around the object to determine the flux of radiation leaving the object we can visualize why this is the case.

Looking at the object from each point on the gaussian surface, its surface contours can not be determined, only its outline. Being a perfect black body, it would also appear uniform in intensity. The radiation it receives from the sphere does not depend on the surface area it sees, but rather the cross sectional area. This is true for every point on the gaussian surface.

Therefore, the radiation emitted away from the object, in total, does not depend on the surface area at all, but the integration of all the cross sections visible from every point on the gaussian surface.

For the case of a dimple, there is no point on the gaussian surface that will see an increase in cross sectional area. The surface area has increased, but the cross sectional area, and therefore radiation output, can only decrease in this case.

This works the other way too, of course, and can be observed clearly when looking at radiation delivered from the Sun to a spherical planet which is a great distance from the Sun. As pictured here:

$_{Source}$

This is further described by principles of irradiance. As described on this website:

The surface area of the sphere is not the factor that determines the amount of absorbed power. Rather, it is the cross-sectional area A which provides the "target size" for intercepting the [radiation]...

As absorbing or emitting is just a direction change, it's clear that surface area is not a factor for emitting radiation either.

Answer 5

I had thought that a golf ball would radiate a tiny bit more energy per unit time away from itself than its smooth counterpart. Although the rate of radiation per unit surface area is the same for both, it seemed to me that the greater surface area of the golf ball, and the configuration of the dimples in its surface, would result in slightly more energy being radiated away than from a smooth sphere of equal radius.

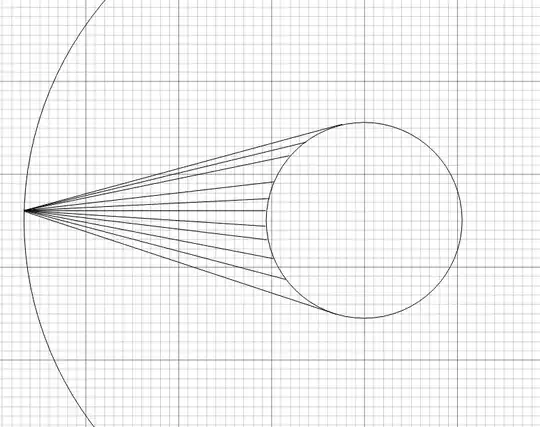
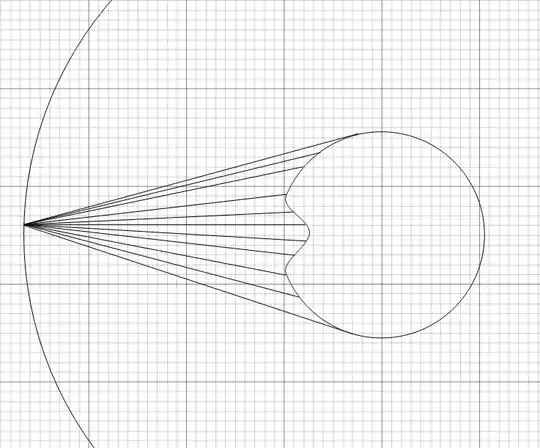
If each dimple in the golf ball, I thought, were no greater than an inverted hemisphere of whatever radius describes the sphere of which it is a cap, more than 50% of radiation emitted by the surface inside the dimple would be radiated away from the golf ball.

Consider a perpendicular to the tangent at each point on the surface of the dimple. All perpendiculars with the exception of those at the horizon of the dimple will clear the horizon. Thus, they will not be reabsorbed.

Consider all other possible angles of radiation at each point on the surface of the dimple. 50% of the angles at the lip of the dimple will be reabsorbed. As the points descend into the dimple, the 50% reabsorption rate for all angles OTHER THAN perpendicular to a tangent to the surface of the dimple will be maintained.

I thought that to the extent perpendiculars to tangents at the dimple surfaces exceed perpendiculars to tangents at the continuous spherical surface that would cover the dimple, they would represent extra energy radiated per unit time by a golf ball.

I failed to realize that the perpendiculars emanating from the dimple would be matched in number by points on the smooth surface of a sphere where the dimple would have been.

Radiation from a black body is described by the Stefan/Boltzmann Law (or Stefan's Law), and by Wien's Law. Wien's law says that the frequency of radiated energy increases with temperature. I don't think that's important for this problem.

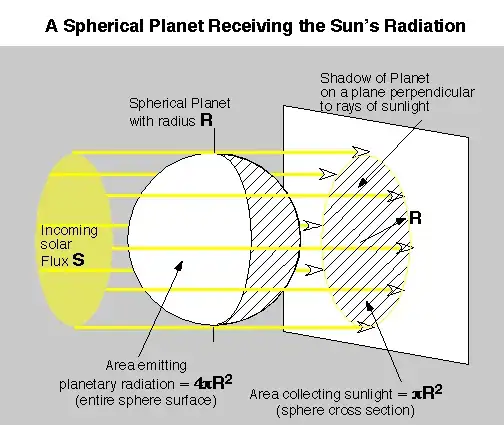
Stefan's Law, which governs total thermodynamic radiation from any black body regardless of shape, is important for this problem. It says that the total energy of heat, across all wavelengths, radiated per unit time, PER UNIT SURFACE AREA, is proportional only to the thermodynamic temperature (taken to the 4th power) of the black body.

Radiant exitance (or radiant flux) emitted from a given surface area = P = dE/dt = ((2*pi^5*k^4)/(15*c^2*h^3)) * A * T^4, where "k" is the Boltzmann constant, "c" is speed of light in a vacuum, "h" is Planck's constant, "A" is surface area, and "T" is thermodynamic temperature of the black body in degrees Kelvin. I left out the emissivity index, which we assume to be 1 as it's a black body, and the ambient temperature, which we assume will have no effect on this problem.

As you can see, the only variables for amount of power emitted per unit time are surface area and temperature.

But although a golf ball has more surface area, and is bound to radiate more energy per unit time per unit surface, all the excess energy will be reabsorbed by the golf ball. Surface area matters. The greater the surface area, the more total heat will be radiated per second. But cross section trumps surface area for energy radiated away and not reabsorbed.

Answer 6

Without resorting to overt mathematics, it's clear that dimples won't help. Consider a radiating surface with uniform luminosity. Place a convex hemisphere with the same luminosity on the surface. What will it look like?

Consider the sun. We can only see one half of it, so it is effectively a hemisphere. It is not quite a perfect lambertian radiator, but it's pretty close, and it appears as a disk of almost uniform brightness. So a bump on a surface will look like a flat patch of the same brightness.

From symmetry, exactly the same effect will be seen with a concave hemisphere - ie, a dimple.

So a dimpled blackbody radiator will appear to be smooth, and dimples don't change the total radiated power.

This is not true for non-lambertian radiators, and real-world surfaces are not perfectly lambertian, but in this ideal case, dimples don't count.

Oh, well, there is a slight difference in the case of bumps rather than dimples - the apparent diameter of the body increases by some fraction of the height of the bumps, so there is a slight increase in radiation for this case. Likewise, the apparent diameter of the sphere is diminished by the slight loss of the "caps" for the dimples, and this will slightly reduce total radiation, but I doubt that's under consideration here.