What speeds are "fast" enough for one to need the relativistic velocity addition formula?

Question

In this question the accepted answer says:

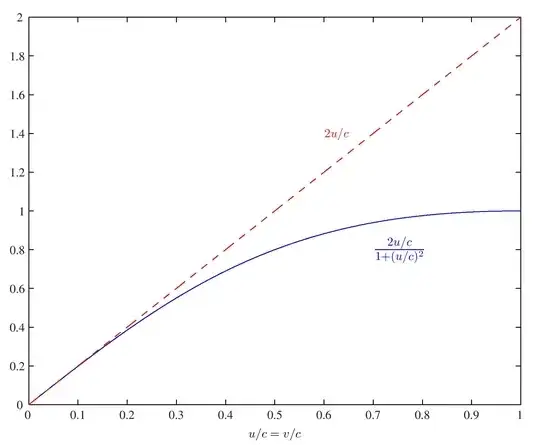
For objects moving at low speeds, your intuition is correct: say the bus move at speed $v$ relative to earth, and you run at speed $u$ on the bus, then the combined speed is simply $u+v$.

But, when objects start to move fast, this is not quite the way things work. The reason is that time measurements start depending on the observer as well, so the way you measure time is just a bit different from the way it is measured on the bus, or on earth. Taking this into account, your speed compared to the earth will be $\frac{u+v}{1+ uv/c^2}$. where $c$ is the speed of light. This formula is derived from special relativity.

What is "fast" in this answer? Is there a certain cutoff for when it stops being $u+v$ and becomes $\frac{u+v}{1+ uv/c^2}$?

Answer 1

For simplicity, consider the case $u=v$. The "slow" formula is then $2u$ and the "fast" formula is $\frac{2u}{1+(u/c)^2}$. In the plot you can see these results in units of $c$. The "slow" formula (red/dashed) is always wrong for $u\ne0$, but it is good enough [close enough to the "fast" formula (blue/solid)] for small $u/c$. The cutoff you choose depends on the accuracy required. When $u<c/10$ then the difference is only likely to be important for high precision work.

A series expansion about $u=v=0$ shows the "slow" formula as the first term and that the corrections are small for $uv \ll c^2$:

$$ \frac{u + v}{1+uv/c^2} = (u + v)\left[1-\frac{uv}{c^2} + \left(\frac{uv}{c^2}\right)^2 + O\left(\frac{uv}{c^2}\right)^3\right] $$

Answer 2

I'm usually a little more specific with my students. Let's consider a car traveling down the highway at $\rm 30\,m/s \approx 60\,mph$. Then the denominator in the relativistic formula is something like $$ 1 + \left(\frac vc\right)^2 = 1 + \left( \frac{30\rm\,m/s}{3\times10^8\rm\,m/s} \right)^2 = 1 + 10^{-14} $$ In your car, then, the difference between Galilean and relativistic velocity addition starts in the fourteenth decimal place. Do you know the speed of your car to fourteen decimal places? This is where they laugh with me.

It's common in experiments to ignore percent-level errors — that is, to trust a number to about three decimal places. Errors this size start to appear between classical and relativistic dynamics when you have $v/c \approx 0.1$, so that's a common cutoff for "fast."

Note that if you can't ignore percent-level corrections, your definition of "fast" changes. For example, a satellite in low-Earth orbit has a speed of $$ v = \frac{2\pi R_\oplus}{90\rm\,minutes} \approx 7500\,\mathrm{m/s} \approx 2\times10^{-5}c $$ and so has relativistic corrections $(v/c)^2 \approx 10^{-10}$ beginning roughly in the tenth decimal place. In the Global Positioning System (GPS), the total relativistic correction of about $38\rm\,\mu s/day \approx 5\times10^{-10}$ is about at this level as well, as is the centimeter-scale precision $$ \frac{1\rm\,cm}{26\,000\rm\,km} \approx 4\times10^{-10} $$ which is occasionally claimed for military-grade GPS hardware.

Answer 3

Actually, regardless of the velocity of the objects in concern, the 'velocity addition' formula is always $\frac{u+v}{1+uv/c^2}$.

There is no transition point where the formula changes from $u+v$ to the special relativity one. Its just that the difference you get in both the formulas at 'low velocities' is very very negligible. $c^2$, in $m^2/s^2$, is $9*10^{16}$. The average speed of a bus is $3.6$ $m/s$. Even for much larger $u,v$ values than that, $uv/c^2$ is negligible. This is why the formula is not of much use in low velocity cases. The significance is observed when $uv/c^2$ is a significant portion of $1$.

Answer 4

The "fast" formula is always the correct one.

A "fast" speed is one that is comparable to the speed of light. However, when both the speeds involved are much smaller than the speed of light, the "slow" formula is a very good approximation.

Answer 5

When does a object go fast [enough to require the use of $\frac{u+v}{1+ uv/c^2}$]?

When you are approaching light speed.

How fast do you need to go to be "approaching" light speed?

That depends on the precision.

The key is that $\frac{u+v}{1+ uv/c^2}$ always works. However, it's not exactly simple, so generally we like to use an approximation: $u+v$. This approximation is rather accurate, unless you start getting close to the speed of light. Unless you require high precision, you should be fine using $u+v$ as long as $u < 0.1 * c$ and $v < 0.1 * c$.

Disclaimer: I think everything hd already been said, I just tried to reword it so it more accurately addresses the question.

Answer 6

Other answers have effectively, or actually, said when you're dealing with $0.1 c$ or above is when you should be considering relativistic effects.

You can see this by just slightly rearranging the $\frac{u+v}{1+ uv/c^2}$ formula:

$$\frac{u+v}{1+ uv/c^2}=\frac{u+v}{1+ (\frac{u}{c})(\frac{v}{c})}$$

And from there you can see while both $u$ and $v$ are $\lt 0.1 c$ the variance is less than $1\%$.

Of course, you can also use this to see $(\frac{u}{c})^2$ is the relativistic correction mentioned in Rob's answer.