What is the Vector/Cross Product?

Question

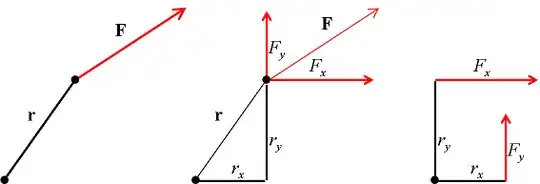
I have decided to start learning physics before I am required to take the class in 11th grade so that I will be ahead of my classmates. I found a cheap physics book on amazon and ordered it but complications occurred when it introduced the Vector/Cross Product. It gives the following equation:

$$\mathbf{A} \times \mathbf{B} = \begin{bmatrix} A_y B_z - A_z B_y \\ A_z B_x - A_x B_y \\ A_x B_y - A_y B_x \end{bmatrix} $$

But it doesn't give any further information such as where the numbers come from. I found the Dot Product to be fairly strait forward while the arrangement of the numbers in this equation seem random at best so I am asking:

• Why are the values of the two vectors arranged as they are in this equation?

Answer 1

In mechanics the vector cross product is used to transform a force at a distance into a moment, and a rotation about an axis into linear velocity

$$ \mathbf{M} = \mathbf{r} \times \mathbf{F} \\ \mathbf{v} = \mathbf{r} \times \mathbf{\omega} $$

If you project those vectors into any plane, you will see that each component of force (or rotation) is multiplied with the perpendicular distance to it (called a moment arm). When combined in 3D the aforementioned expression for cross product is found.

For example consider the XY plane which yields a component about the Z axis

The torque of the force $F$ at a distance $d$ is found by splitting the distance and force into components. The result is $M_z=r_x F_y -r_y F_x$ which is the same as the 3rd component of the cross product. If you do the same on all basic planes of projection you will end up with the cross product expression.

Often I view the vector cross product, not as a binary operation (between two vectors), But as an operator on a vector with

$$ \mathbf{A} \times \mathbf{B}=[\mathbf{A} \times] \mathbf{B} = \begin{vmatrix} 0 & -A_z & A_y \\ A_z & 0 & -A_x \\ -A_y & A_x & 0\end{vmatrix} \begin{bmatrix} B_x \\ B_y \\ B_z\end{bmatrix} =\begin{bmatrix} A_y B_z - A_z B_y \\ A_z B_x - A_x B_y \\ A_x B_y - A_y B_x \end{bmatrix}$$

(See Vector Cross Product Skew Symmetric Matrix)

Answer 2

A vector product of two vectors is also called a cross product. As you may know, one way of describing a vector, as opposed to defining a vector is "a quantity which has magnitude and direction." In 3-dimensional space, one can specify a vector as the sum of $x, y,$ and $z$ components of parts. We can write $$\vec{A} = (A_x, A_y, A_z) \text{ or } A_x\hat{i} +A_y\hat{j}+A_z\hat{k}.$$

The $\hat{i}, \hat{j}, \hat{k}$ terms are ways of specifying the $x,y,z$ directions and are useful for calculations..

The vector product has a magnitude equal to the product of the length of one vector and the component of the other vector:$$|\vec{A}\times\vec{B}|=AB\sin\theta,$$ where $A$ and $B$ are the magnitudes of the vectors and $\theta$ is the angle between them. The direction of the vector product is perpendicular to both vectors. That leaves two possible directions, and the conventional direction is to use a right-handed "screw out" rotation of $\vec{A}$ being pushed toward $\vec{B}$.

Without writing all the details of results, $A_xB_x$ and other like-direction component products contribute nothing. That's because the angle $\theta$ between like components is 0, and sin(0)=0. $A_xB_y - A_yB_x$ is the $z$-component and you form the others as permutations of $x,y,z$: $$x,y\rightarrow z,$$ $$y,z\rightarrow x,$$ $$z,x\rightarrow y$$ and reversing the order of the first two yields a negative sign.

Answer 3

A$\times$B is a vector that is perpendicular to both A and B, and its norm (length) is equal to the area of the parallelogram whose sides are the vectors A and B. You can check that that seemingly random expression satisfies both properties.