This is a quick mock-up of how stars are measured using parallax method.
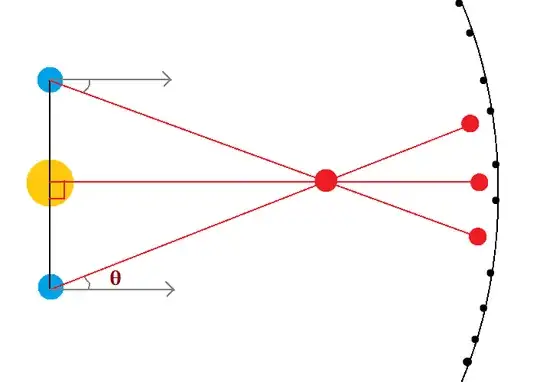
My question is :
How on earth (literally) do we measure the anfle $\theta$?
Is theta measured from the zenith of Earth? ie, Are the gray lines the zenith of earth?
This is a quick mock-up of how stars are measured using parallax method.

My question is :
How on earth (literally) do we measure the anfle $\theta$?
Is theta measured from the zenith of Earth? ie, Are the gray lines the zenith of earth?
The positions of stars on the sky are defined against a co-ordinate reference frame that is ultimately defined by the positions of very distant radio sources (quasars at high redshift) that are assumed to be "stationary" in terms of their celestial grid co-ordinates (see International Celestial Reference Frame)
All stars can have their positions precisely measured on this system. A nearby star will have a position that varies with time. There are TWO reasons for this. One is the parallax, as shown in your diagram.
If parallax were the only factor, then the parallax angle $\theta$ is half the change in position of the star on the standard coordinate system over 6 months. If the top of your diagram is Dec 21 and the bottom were June 21 (covering half the Earth's orbit), then the grey lines would represent the position of the nearby star on March 21 (i.e. half way in between). Of course in reality this has to be corrected (slightly) for the non-circularity of the Earth's orbit - and the "annual parallax" of a star is defined as the angle $\theta$ that would be seen for an average Earth orbital radius.
The other factor is proper motion (not shown on your diagram). This is caused by the relative motion of the solar system with respect to nearby stars. This causes the positions of nearby stars to change (almost) linearly with time - ie they "drift" across the sky. Very often, this effect completely dominates the parallax effect, so the measurement of two positions even 6 months apart cannot distinguish between parallax and proper motion. Therefore in practice, what you do is take a series of measurements and with a bit of simple analysis, take out the drift due to proper motion and isolate the parallax angle as shown in your diagram.
Possibly the following diagram would help. It tracks the position of a nearby star (the nearest - Proxima Centauri) over several years. The general drift in position against the background (and assumed much more distant) star field is the proper motion, but the oscillations are due to the orbital motion, and their semi-amplitude, expressed in terms of angular displacement on the sky, corresponds to the angle $\theta$ in your diagram.
EDIT: Possibly you are not following that a separation between two points on an astronomical image corresponds to an angular separation. ie given two positions (right ascensions and declinations), you use a simple trigonometric formula to calculate the angle between these two directions. So $\theta$ would be approximately the angular separation between the calibrated stellar position on Dec 21 and its position on March 21 (ignoring the complication of proper motion).
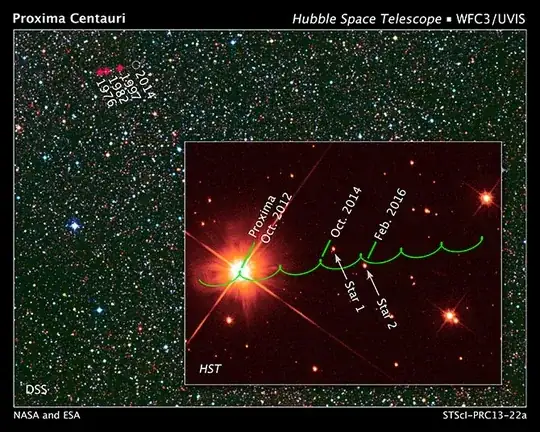
$\theta$ is half the difference in direction of 2 measurements of the position of the star taken 6 months apart.