In Radiometry, radiance (L) is defined as flux density per unit area per unit solid angle. If we move further along a ray, away from a point, shouldn't the radiance decrease? I am unable to grasp an intuitive reason for the statement:
Radiance remain constant along rays of light through empty space.
Any explanation in this regard would be highly appreciated.
Imagine you start right next to a star. As you move away from the star, the intensity of the light $I$ (in $W/m^2$) goes down depending on distance $r$ following an inverse-square law:
$$I\ \propto\ \frac{1}{r^2}$$
but the solid angle $\Omega$ (in $sr$) also decreases in the same proportion:
$$\Omega\ \propto\ \frac{1}{r^2}$$
Therefore since radiance $L$ (in $W/m^2\cdot sr^{-1}$) is intensity per unit solid angle:
$$L\ \propto\ \frac{I}{\Omega}$$
the $r^2$ cancels out and radiance does not depend on distance.
I think the clearest way to understand "why radiance is constant" along a ray of light is using the law of conservation of energy.
$$ \text{d}^3Q_{2\leftarrow 1} = L_2 \underbrace{\text{d}A_{2\perp}}_{\text{(3)}} \underbrace{\text{d}\omega_{1(2)}}_{\text{(4)}} \text{d}t, $$ where $$\begin{align} (1) &\text{ Area "sending" light from }x_1\text{ to }x_2\\ &\qquad \text{d}A_{1\perp} = \text{d}A_1 \cos \beta_1 \\ (2) &\text{ Solid angle including } x_2 \text{ (i.e. d}A_2\text{) into which light is "sent" from }x_1\\ &\qquad \text{d}\omega_{2(1)} = \tfrac{\text{d}A_2 \cos \beta_2}{r^2} \\ (3) &\text{ Area "collecting" light from }x_1\text{ at }x_2\\ &\qquad \text{d}A_{2\perp} = \text{d}A_2 \cos \beta_2 \\ (4) &\text{ Solid angle from which light is collected from at }x_2\text{, including }x_1\text{ (i.e. d}A_1\text{).}\\ &\qquad \text{d}\omega_{1(2)} = \tfrac{\text{d}A_1 \cos \beta_1}{r^2} \\ \end{align} $$
Only terms (2) and (4) have "$\tfrac{1}{r^2}$"-dependency, and they cancel out. Also other terms cancel out leaving
$$ L_1 = L_2 $$ That is, radiance is constant along a ray of light. □
Let us consider two infinitesimally small patches $\text{d}A_1$ and $\text{d}A_2$ located at $x_1$ and $x_2$, respectively. The ${n}_1$ and ${n}_2$ are the normal vectors and $\beta_1$ and $\beta_2$ angles between the normals and the vector $x_1 \rightarrow x_2$.
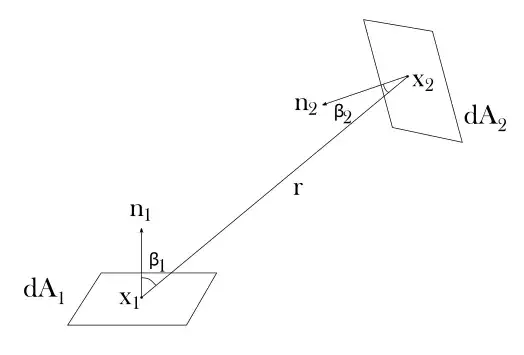
Also recall the definition of radiance
$$ L = L(\text{location}, \text{direction}) \equiv \dfrac{\text{d}\Phi} {\text{d}A_\perp\text{d}\omega} \qquad \text{[W/m2/sr]}, $$ where $\Phi$ is radiant flux, defined as $$ \Phi = \dfrac{\text{d}Q}{\text{d}t} \qquad \text{[W]}, $$ $Q$ is radiant energy [J], and $\omega$ is the solid angle $$ \omega = \dfrac{A_{\text{sph}}}{r^2} $$ where $A_{\text{sph}}$ is spherical surface area, but with insinitesimally small $\text{d}\omega$ is can be considered to be flat surface $$ \text{d}\omega = \dfrac{\text{d}A}{r^2} $$ $r$ is distance between point of observation and the area $A$, and $A_\perp$ means area perpendicular to the direction of radiation. Now we assume lossless medium, and that rays move straight.
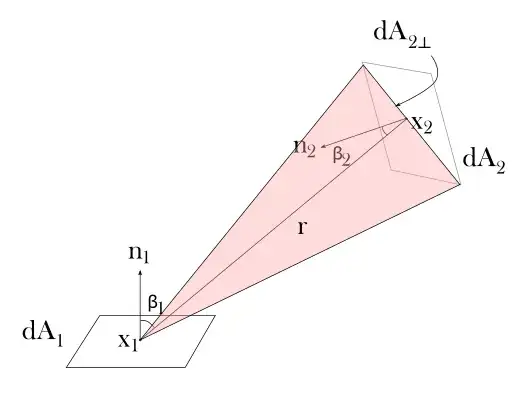
Now that was a lot of definitions. Let's put them into use. Energy leaving the point $x_1$ (i.e. the infinitesimally small area $\text{d}A_1$) towards the point $x_2 $ (i.e. the infinitesimally small area $\text{d}A_2$) is, from definition of radiance
$$ \text{d}^3Q_{1\rightarrow 2} = L(x_1, x_1 \rightarrow x_2) \text{d}A_{1\perp}\text{d}\omega_{2(1)} \text{d}t $$
Here $\text{d}A_{1\perp}$ is area of $\text{d}A_1$ perpendicular to the direction "$x_1 \rightarrow x_2$";
$$ \text{d}A_{1\perp} = \text{d}A_1 \cos \beta_1 $$ and $\text{d}\omega_{2(1)}$ is the infinitesimally small solid angle spanned by $\text{d}A_2$ when looking at $x_1$, i.e.
$$ \text{d}\omega_{2(1)} = \dfrac{\text{d}A_{2\perp}}{r^2} = \dfrac{\text{d}A_{2} \cos \beta_2 }{r^2} $$
The $\text{d}\omega_{2(1)}$ is the red solid angle in the figure below. Combining the above, we get for the energy
$$ \text{d}^3Q_{1\rightarrow 2} = L(x_1, x_1 \rightarrow x_2) \dfrac{\cos \beta_1 \text{d}A_1 \cos \beta_2 \text{d}A_2}{r^2} \text{d}t $$
The energy arriving to $\text{d}A_2$ from $x_1$ can be calculated similarly. This is the energy collected from the red solid angle $\text{d}\omega_{1(2)}$, that is, the solid angle spanned by $\text{d}A_1$ at $x_2$.
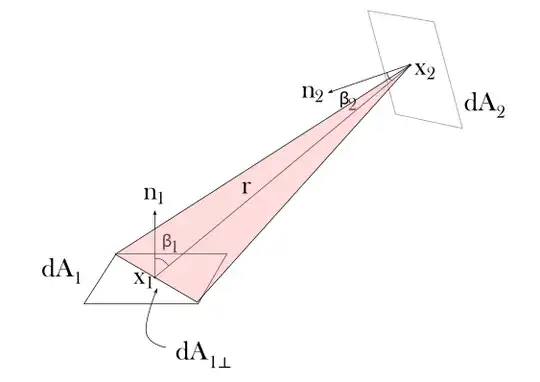
$$ \text{d}^3Q_{2 \leftarrow 1} = L(x_2, x_1 \rightarrow x_2) \text{d}A_{2\perp}\text{d}\omega_{1(2)} \text{d}t $$ which is, since $\text{d}\omega_{1(2)} = \text{d}A_1 \cos\beta_1 /r^2$ $$ \text{d}^3Q_{2 \leftarrow 1} = L(x_2, x_1 \rightarrow x_2) \dfrac{\cos \beta_1 \text{d}A_1 \cos \beta_2 \text{d}A_2}{r^2} \text{d}t $$
Now we have calculated how much energy there is transferred in time $\text{d}t$ from point $x_1$ to point $x_2$ at arbitrary distance $r$. Note that we have only considered energy transfer between to points, along one ray (the areas are infinitesimally small)! We know that energy is conserved (since the medium is lossless), and therefore
$$ \text{d}^3Q_{1\rightarrow 2} = \text{d}^3Q_{2 \leftarrow 1} $$ which is $$ L(x_1, x_1 \rightarrow x_2) \dfrac{\cos \beta_1 \text{d}A_1 \cos \beta_2 \text{d}A_2}{r^2} \text{d}t = L(x_2, x_1 \rightarrow x_2) \dfrac{\cos \beta_1 \text{d}A_1 \cos \beta_2 \text{d}A_2}{r^2} \text{d}t $$ and therefore $$ L(x_1, x_1 \rightarrow x_2) = L(x_2, x_1 \rightarrow x_2) $$
Note that we could have placed the point $x_1$ and $x_2$ anywhere and the distance $r^2$ could be anything. That means, the radiance will be constant along a ray of light.
