This refers to a previous question re: Solar Cell Systems and as part of the answer the statement:
If we concentrated sunlight to [the] maximum amount 42600× was given.
My questions are:
By what physical method is this achieved?
How do we know that figure of 42600x is the theoretical (or practically achievable) maximum limit of concentration?
The sun is an extended source. This means that it occupies a definite solid angle in the sky $\omega = 6.8\times 10^{-5} Sr$.
To visualise this (not to scale), let's say that the black area in the following diagram is the angular extent of the sun as seen from the surface of the Earth (ignore the other labels),
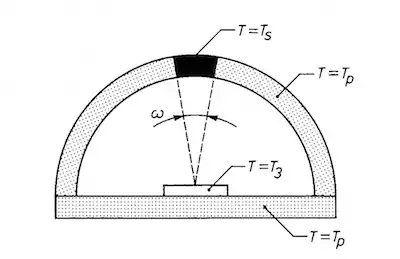
What happens when we concentrate sunlight from the perspective of the white plate in the diagram? Answer: the sun looks bigger! It begins to fill more of the "sky".
When light rays are traveling from all angles towards the plate then we have reached maximum concentration.
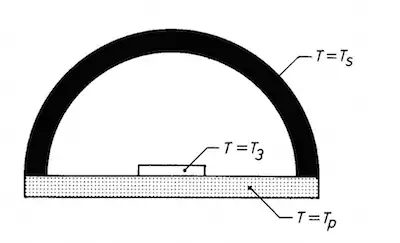
So maximum concentration is defined as when the true angular size of the sun is made to fill a hemisphere solid angles. The angular size of the sun is approx. $\theta_s = 0.2666^{\circ}$, note this is the half-angle, therefore performing the solid angle integration yields,
$$ X_{2D} = \frac{\iint_{2\pi}\cos\theta\ d\omega}{\iint_{\omega_s}\cos\theta\ d\omega} = \frac{\int_0^{2\pi}d \phi \int_0^{\pi/2} \cos\theta\sin\theta\ d \theta }{\int_0^{2\pi}d \phi \int_0^{\theta_s} \cos\theta\sin\theta\ d \theta} = \frac{\frac{2\pi}{2}}{\frac{2\pi\sin^2\theta_s}{2}} = \frac{\pi}{6.8\times 10^{-5} Sr} = 46200\times $$
This assumes that we can change the angular extent of light in both $x$ and $y$ and focus to a point. If instead you can only focus to a line then the limit is much smaller,
$$ X_{1D} = 220\times $$
You can actually do this a bit more simply (or at least without integrations).
Luminance is invariant in geometrical optics. That is, the brightness of an image cannot be brighter than the source.
The radius of the sun is 0.6958 x 10^6 meters. The radius of the earth's orbit is a mean of 149.6 x 10^6. Then the brightness at the surface of the sun is the square of the ratios, or (149.6 /.6958)^2, or 46,228 as bright as it is at earth orbit, and this represents the best performance of a solar concentrator.
