What should be the intuitive explanation of wave equation?

Question

$$\dfrac {\partial^2 y}{{\partial x}^2} = \dfrac{1}{v^2} \dfrac{\partial^2 y}{{\partial t}^2}$$ is the wave equation in one dimension. But what should be the intuition behind it? That is, what meaning does this equation convey?

This equation is derived from $$v \dfrac{\partial y}{\partial x} = \dfrac{\partial y}{\partial t}$$ which can be intuitively explained as the transverse velocity of the element(string wave) at a point is directly proportional to the slope of the wave at that point. But, if I square to get the wave equation, then what should be the explanation? What is meant by $$\dfrac{\partial^2 y}{{\partial x}^2} \quad \& \quad \dfrac{\partial^2 y}{{\partial t}^2}$$? Just need a good intuitive lucid explanation.

Answer 1

The "intuition" here is that the wave equation is the equation for a general "disturbance" that has a left- and a right-travelling component, i.e. spreads without any preferred direction given by the equation of motion.

Observe that $$ \left(v^2 \frac{\partial^2}{\partial x^2} - \frac{\partial^2}{\partial t^2}\right) y = 0$$ can be factored as (which is what you probably mean by "squaring" in the question) $$ \left(v\frac{\partial}{\partial x} + \frac{\partial}{\partial t}\right)\left(v\frac{\partial}{\partial x} - \frac{\partial}{\partial t}\right) y = 0$$ implying $$ \left(v\frac{\partial}{\partial x} + \frac{\partial}{\partial t}\right)y = 0 \quad\vee\quad \left(v\frac{\partial}{\partial x} - \frac{\partial}{\partial t}\right) y = 0$$ where it is easy to see that $y(x,t) \equiv y(x - vt)$ and $y(x,t) \equiv y(x + vt)$ are solutions, respectively. Since $v$ is assumed positive, $x-vt$ becomes smaller as the time $t$ passes (whatever $y$ describes is travelling to the right in the usual coordinate system), and similarily, $x+vt$ is travelling to the left. By linearity, the general solution is a sum of left- and right-movers, i.e. $y(x,t) \equiv y_R(x - vt) + y_L(x + vt)$.

The initial conditions $y(x,0) = f(x)$ and $\frac{\partial}{\partial t}y(x,0) = g(x)$ for arbitrary functions of position $f,g$ fully specify the solution by d'Alembert's formula: $$ y(x,t) = \frac{1}{2}\left[f(x-vt) + f(x+vt) + \frac{1}{v}\int_{x-vt}^{x+vt}g(z)\mathrm{d}z\right]$$ where (roughly) $f$ corresponds to the shape of the disturbance and $g$ to the way it will spread. Note that, in particular, for $g = 0$ and $f = \sin$, we obtain just a standing wave.

Answer 2

First of all, $\frac{\partial^2 y}{\partial x^2}$ and $\frac{\partial^2 y}{\partial t^2}$ are second partial derivatives of $y(x,t)$ with respect to $x$ and $t$. So you can't obtain the wave equation from the first order equation

$$v \frac{\partial y}{\partial x} = \frac{\partial y}{\partial t}$$

by squaring it in an algebraic sense. Also the square of the differential operator

\begin{equation} v \frac{\partial}{\partial x}-\frac{\partial}{\partial t} \end{equation}

is not the correct one. I will comment about that at the end.

About the intuitive explanation: a piece of the string is subject to a force (and, as a consequence, to an acceleration $\partial^2 y/\partial t^2$) which is proportional to its curvature, which is measured for small slopes by the second derivative $\partial^2 y/\partial x^2$. The reason for this is that at the edges of the string the tension gives tangent forces (see the figure)

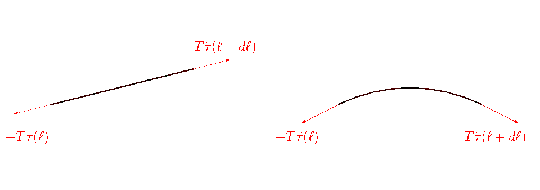
In the first approximation you neglect the second derivative, and the piece of string is approximated by a segment. In this case there is no net force, because the effects of the tension at the two edges cancel (figure on the left). In a second approximation the piece of string is curved (figure on the right) and you get a net transverse force.

Note that you can write the wave equation in the form

$$\left(\frac{\partial}{\partial x}-\frac{1}{v} \frac{\partial}{\partial t} \right)\left(\frac{\partial}{\partial x}+\frac{1}{v} \frac{\partial}{\partial t} \right)y(x,t)=0$$

by factorizing the differential operator. You see that $y(x,t)$ is a solution of the wave equation if it is a solution of

$$\left(\frac{\partial}{\partial x}-\frac{1}{v} \frac{\partial}{\partial t} \right)y(x,t)=0$$

or if it is a solution ofs

$$\left(\frac{\partial}{\partial x}+\frac{1}{v} \frac{\partial}{\partial t} \right)y(x,t)=0$$

In the first case the most general solution is $y(x,t)=F(x+vt)$, in the second $y(x,t)=G(x-vt)$, where $F$ and $G$ are arbitrary functions. The first equation is equivalent to the one you are trying to derive the wave equation from: it describes an arbitrary wave which moves in the left direction. But there are also waves which moves in the right direction, which are solution of the second equation. The correct wave equation contains the product of both the first order differential operators, and not the square of one of them.